第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
同学们,你们还记得有理数的本质是什么吗?一天,$\sqrt{2}$看见一群数字:$2,\sqrt{9},-\frac{1}{4},0,-5$,$0.3\cdots\cdots$在花园里捉迷藏,于是走过去想跟它们一起玩. 可是,其中的一个数字说$\sqrt{2}$和它们不一样,不愿意和它一起玩. 这到底是怎么回事呢?你能说清楚吗?
答案:
$\sqrt{2}$是无理数,与其他有理数不同。
1. 无理数:
无限不循环小数
叫做无理数.
答案:
1. 无限不循环小数
2. 实数:
有理数
和无理数
统称为实数.
答案:
2. 有理数 无理数
3. 实数的分类:
(1)
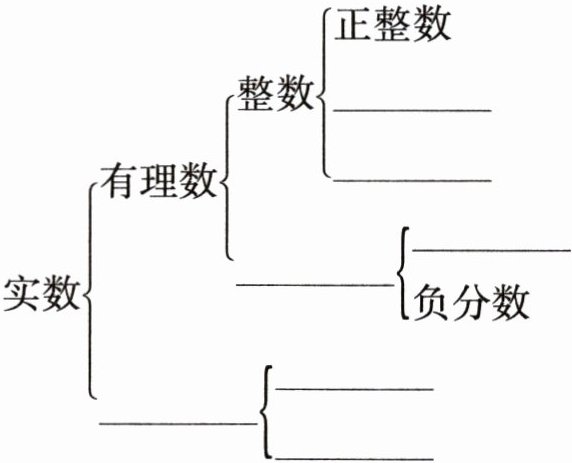
$实数 \left\{\begin{array}{l}$$有理数 \left\{\begin{array}{l}整数 \left\{\begin{array}{l}正整数 \$_________$ \$_________$\end{array}\right. \$_________$ \left\{\begin{array}{l}$$ \\负分数$$\end{array}\right.\end{array}\right. \$_________$ \left\{\begin{array}{l}$_________$ \$_________$\end{array}\right.\end{array}\right.$
(2) 实数按正负性分类:
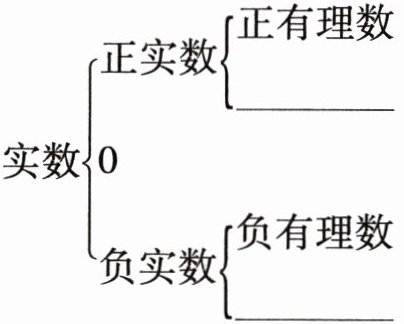
$实数 \left\{\begin{array}{l}正实数 \left\{\begin{array}{l}$$正有理数 \$_________$\end{array}\right. \\0 \\负实数 \left\{\begin{array}{l}负有理数 \$_________$\end{array}\right.\end{array}\right.$
(1)
略
实数按定义分类:
$实数 \left\{\begin{array}{l}$$有理数 \left\{\begin{array}{l}整数 \left\{\begin{array}{l}正整数 \$_________$ \$_________$\end{array}\right. \$_________$ \left\{\begin{array}{l}$$ \\负分数$$\end{array}\right.\end{array}\right. \$_________$ \left\{\begin{array}{l}$_________$ \$_________$\end{array}\right.\end{array}\right.$
(2) 实数按正负性分类:

$实数 \left\{\begin{array}{l}正实数 \left\{\begin{array}{l}$$正有理数 \$_________$\end{array}\right. \\0 \\负实数 \left\{\begin{array}{l}负有理数 \$_________$\end{array}\right.\end{array}\right.$
答案:
(1)
整数:
正整数
零
负整数
分数:
正分数
负分数
无理数:
正无理数
负无理数
(2)
正实数:
正有理数
正无理数
负实数:
负有理数
负无理数
(1)
整数:
正整数
零
负整数
分数:
正分数
负分数
无理数:
正无理数
负无理数
(2)
正实数:
正有理数
正无理数
负实数:
负有理数
负无理数
4. 实数与数轴上的点
一一对应
,即数轴上的每一个点必定表示一个实数;反过来,每一个实数(有理数或无理数)都可以用数轴上的一个点来表示.
答案:
4. 一一对应
例题 如图是一个无理数筛选器的工作流程图,请回答相关问题.
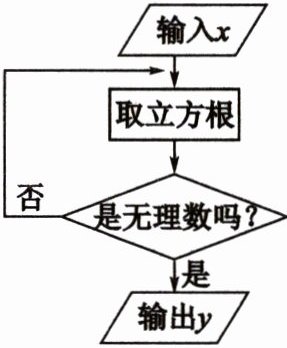
(1) 当$x = 8$时,$y$的值为
(2) 当输出的$y$值是$\sqrt[3]{3}$时,输入的$x$值唯一吗?若不唯一,请写出其中两个输入的$x$值.
(3) 是否存在输入某个$x$值后,却始终输不出$y$值?如果存在,写出所有满足要求的$x$值;如果不存在,请说明理由.
答案:(1) $\sqrt[3]{2}$
(2) 不唯一,如输入的$x$值可以是$3$或$27$.
(3) 当输入的数是$-1,0,1$时,取它们的立方根始终分别是$-1,0,1$,
$\therefore$ 当输入的$x$分别是$-1,0,1$时,始终输不出$y$值.
【解析】(1) 依据运算规则$\sqrt[3]{8} = 2$,$2$是有理数,再次输入$2$计算得$\sqrt[3]{2}$,为无理数,即$y = \sqrt[3]{2}$.
(2) 根据运算规则进行反向思考,即可求得无数个满足条件的数,如$3,27,27^3$等.
(3) 根据运算规则,若无法输出$y$的值,则意味着求立方根后的数始终可以开立方,即为
特殊的有理数:$-1,0,1$.
方法点拨 本题主要考查对无理数与立方根的理解,正确理解其运算规则是解题关键.

(1) 当$x = 8$时,$y$的值为
$\sqrt[3]{2}$
.(2) 当输出的$y$值是$\sqrt[3]{3}$时,输入的$x$值唯一吗?若不唯一,请写出其中两个输入的$x$值.
(3) 是否存在输入某个$x$值后,却始终输不出$y$值?如果存在,写出所有满足要求的$x$值;如果不存在,请说明理由.
答案:(1) $\sqrt[3]{2}$
(2) 不唯一,如输入的$x$值可以是$3$或$27$.
(3) 当输入的数是$-1,0,1$时,取它们的立方根始终分别是$-1,0,1$,
$\therefore$ 当输入的$x$分别是$-1,0,1$时,始终输不出$y$值.
【解析】(1) 依据运算规则$\sqrt[3]{8} = 2$,$2$是有理数,再次输入$2$计算得$\sqrt[3]{2}$,为无理数,即$y = \sqrt[3]{2}$.
(2) 根据运算规则进行反向思考,即可求得无数个满足条件的数,如$3,27,27^3$等.
(3) 根据运算规则,若无法输出$y$的值,则意味着求立方根后的数始终可以开立方,即为
特殊的有理数:$-1,0,1$.
方法点拨 本题主要考查对无理数与立方根的理解,正确理解其运算规则是解题关键.
答案:
1. $\sqrt[3]{2}$
2. 不唯一,如输入的$x$值可以是$3$或$27$.
3. 当输入的数是$-1,0,1$时,取它们的立方根始终分别是$-1,0,1$,$\therefore$ 当输入的$x$分别是$-1,0,1$时,始终输不出$y$值.
2. 不唯一,如输入的$x$值可以是$3$或$27$.
3. 当输入的数是$-1,0,1$时,取它们的立方根始终分别是$-1,0,1$,$\therefore$ 当输入的$x$分别是$-1,0,1$时,始终输不出$y$值.
查看更多完整答案,请扫码查看


