《2025年新课程问题解决导学方案八年级数学上册华师大版》

11. 著名的赵爽弦图（如图 1，其中四个直角三角形较长的直角边长都为 $ a $，较短的直角边长都为 $ b $，斜边长都为 $ c $）中，大正方形的面积可以表示为 $ c^{2} $，也可以表示为 $ 4×\frac{1}{2}ab + (a - b)^{2} $，由此推导出重要的勾股定理：若直角三角形两条直角边长分别为 $ a $、$ b $，斜边长为 $ c $，则 $ a^{2} + b^{2} = c^{2} $.
（1）图 2 为美国第二十任总统加菲尔德的“总统证法”，请你利用图 2 推导勾股定理.
（2）如图 3，在一条东西走向河流的一侧有一村庄 $ C $，河边原有两个取水点 $ A $、$ B $，其中 $ AB = AC $，由于某种原因，由 $ C $ 到 $ A $ 的路现在已经不通，该村为了方便村民取水，决定在河边新建一个取水点 $ H $（点 $ A $、$ H $、$ B $ 在同一条直线上），并新修一条路 $ CH $，且 $ CH \perp AB $，已知 $ CH = 1.6 $ 千米，$ HB = 1.2 $ 千米，求新路 $ CH $ 比原路 $ CA $ 少多少千米？
（3）在第（2）问中，若 $ AB \neq AC $ 时，$ CH \perp AB $，$ AC = 4 $，$ BC = 5 $，$ AB = 6 $，设 $ AH = x $，求 $ x $ 的值.
（第11题图）

答案： 11.
(1)梯形ABCD的面积为
$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$a²+ab+$\frac{1}{2}$b²,
也可以表示为$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c²,
∴ $\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c²=$\frac{1}{2}$a²+ab+$\frac{1}{2}$b²,
即a²+b²=c².
(2)设CA=x，则AH=x - 1.2.
在Rt△ACH中，CA²=CH²+AH²,
即x²=1.6²+(x - 1.2)².
解得x=$\frac{5}{3}$.
即CA=$\frac{5}{3}$,
CA - CH=$\frac{5}{3}$ - 1.6=$\frac{1}{15}$(千米).
答:新路CH比原路CA少$\frac{1}{15}$千米.
(3)已知AH=x，则BH=6 - x.
在Rt△ACH中，CH²=CA² - AH²,
在Rt△BCH中，CH²=CB² - BH²,
∴ CA² - AH²=CB² - BH²,
即4² - x²=5² - (6 - x)².
解得x=$\frac{9}{4}$.

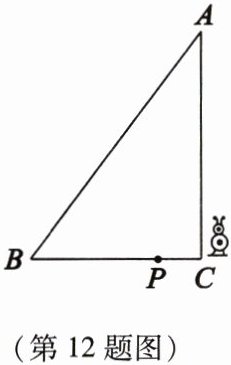
12. 某校机器人兴趣小组在如图所示的三角形场地上开展训练，已知 $ \angle ACB = 90^{\circ} $，$ AB = 10 $，$ BC = 6 $，$ AC = 8 $，机器人从点 $ C $ 出发，按 $ C \to B \to A \to C $ 的方向匀速移动，到点 $ C $ 停止，机器人移动的速度为每秒 $ 2 $ 个单位长度，移动至拐角处调整方向需要 $ 1 $ 秒（即在 $ B $、$ A $ 处拐弯时分别用时 $ 1 $ 秒）. 设机器人所用时间为 $ t $ 秒时，其所在位置用点 $ P $ 表示.（机器人大小不计）
（1）点 $ C $ 到 $ AB $ 边的距离是多少？
（2）是否存在这样的时刻，使 $ \triangle PBC $ 为等腰三角形？ 若存在，求出 $ t $ 的值；若不存在，请说明理由.

答案： 12.
(1)
∵ △ABC是直角三角形，
∴ 点C到AB边的距离
=$\frac{BC·AC}{AB}=\frac{6×8}{10}=4.8$.
(2)存在点P，使△PBC为等腰三角形.
①当点P在BC上时，不符合题意.
②当点P在AB上时，分为三种情况:
a.若BP=BC，根据题意，得
2(t - 1) - 6=6,
解得t=7;
b.若CP=CB，根据题意，得
$(\frac{24}{5})^{2}+(t - 4)^{2}=6^{2}$,
解得t=7.6;
c.若PB=CP，根据题意，得
2(t - 1) - 6=$\frac{1}{2}$×10,
解得t=6.5.
③当点P在AC上时，CB=CP.
根据题意，得
8 - [2(t - 2) - 16]=6,
解得t=11.
综上所述，当t的值为7或7.6或6.5或11时，△PBC为等腰三角形.