《2025年新课程问题解决导学方案八年级数学上册华师大版》

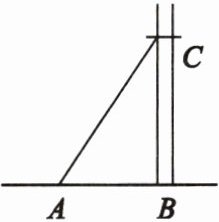
如图，供电局张师傅要安装电线杆，按要求电线杆要与地面垂直，因此，若从离地面8m高的C处向地面拉一条长10m的钢绳，测得地面钢绳固定点到电线杆底部的距离为6m，则张师傅的安装方法是否符合要求？请说明理由。

答案： 符合要求（或具体选择题的答案选项）。

1. 勾股定理的逆定理：如果三角形的三边长a、b、c有关系$a^{2}+b^{2}=c^{2}$，那么这个三角形是直角三角形，且边c所对的角为直角。

答案： 1. $a^{2}+b^{2}=c^{2}$

2. 能够成为直角三角形三条边长的三个正整数，称为勾股数。
常见的勾股数有：①3、4、5；②5、12、13；③7、24、25；④9、40、41；⑤11、60、61；⑥12、16、20；⑦13、84、85；⑧8、15、17；⑨12、35、37。

答案： 2. 正整数

例1 判断满足下列条件的三角形是不是直角三角形：
（1）在△ABC中，∠A=25°，∠C=65°。
（2）在△ABC中，AC=12，AB=20，BC=16。
（3）一个三角形的三条边长a、b、c满足a：b：c=3：4：5。
答案：（1）在△ABC中，∠A=25°，∠B=65°，
∴ ∠C=180°−∠A−∠B=90°。
∴ △ABC是直角三角形。
（2）∵ 12²+16²=20²，即AC²+BC²=AB²，
∴ △ABC是直角三角形，且∠C是直角。
（3）设a=3x，则b=4x，c=5x。
∵ (3x)²+(4x)²=(5x)²，
即a²+b²=c²，
∴ △ABC是直角三角形。
方法点拨 本题考查勾股定理的逆定理和三角形内角和定理，解答本题的关键是明确题意，利用勾股定理逆定理的知识解答。

答案： 答题卡作答：
（1）
在$\triangle ABC$中，已知$\angle A = 25°$，$\angle C = 65°$，
根据三角形内角和为$180°$，
可得$\angle B = 180° - \angle A - \angle C = 180° - 25° - 65° = 90°$。
因此，$\triangle ABC$是直角三角形。
（2）
在$\triangle ABC$中，已知$AC = 12$，$AB = 20$，$BC = 16$，
根据勾股定理的逆定理，若$AC^2 + BC^2 = AB^2$，则$\triangle ABC$是直角三角形，
计算得$12^2 + 16^2 = 144 + 256 = 400 = 20^2 = AB^2$，
因此，$\triangle ABC$是直角三角形，且$\angle C$是直角。
（3）
设三角形的三条边长分别为$a = 3x$，$b = 4x$，$c = 5x$，
根据勾股定理的逆定理，若$a^2 + b^2 = c^2$，则三角形是直角三角形，
计算得$(3x)^2 + (4x)^2 = 9x^2 + 16x^2 = 25x^2 = (5x)^2 = c^2$，
因此，该三角形是直角三角形。

例2 下面四组数中是勾股数的一组是()。
A. 6，7，8
B. 3²，4²，5²
C. 0.5，1.2，1.3
D. 12，16，20
答案：D
【解析】A. 6²+7²≠8²，不能构成勾股数，不符合题意；
B. (3²)²+(4²)²≠(5²)²，不能构成勾股数，不符合题意；
C. 0.5，1.2，1.3不是整数，不能构成勾股数，不符合题意；
D. 12²+16²=20²，能构成勾股数，符合题意。
故选D。
方法点拨 本题考查勾股数，解答此题要深刻理解勾股数的定义。根据勾股数的定义：满足a²+b²=c²的三个正整数，称为勾股数解答即可。

答案： D