《2025年名校课堂九年级数学全一册人教版云南专版》

9. (红河二模)如图，在$Rt\triangle BCO$中，$\angle BCO = 90^{\circ}$，$\angle CBO = 30^{\circ}$，$BO = 2$ cm. 将$\triangle BCO$绕点$O$逆时针旋转得到$\triangle B'C'O$，点$C'$在$BO$的延长线上，则边$BC$扫过区域(图中阴影部分)的面积为 ( )

A.$\pi$ cm²
B.$(\frac{\sqrt{3}}{2} + \pi)$ cm²
C.$2\pi$ cm²
D.$(\frac{\sqrt{3}}{2} + 2\pi)$ cm²

答案： A

10. (昆明官渡区期末)如图，在$Rt\triangle ABC$中，$\angle A = 90^{\circ}$，$\angle B = 30^{\circ}$，$AC = 4$，以$A$为圆心，$AC$长为半径画四分之一圆，则图中阴影部分的面积是__________.(结果保留根号和$\pi$)

答案： $4√3 - \frac{4}{3}\pi$

11. (昆明五华区一模)如图，在扇形$OAB$中，已知$\angle AOB = 90^{\circ}$，$OA = \sqrt{2}$，过$\overset{\frown}{AB}$的中点$C$作$CD \perp OA$，$CE \perp OB$，垂足分别为$D$，$E$，则图中阴影部分的面积为__________.(结果保留$\pi$)
]

答案： $\frac{\pi}{2}-1$

12. (云南民大附中期中)如图，$\triangle ABC$三个顶点的坐标分别为$A(2,4)$，$B(1,1)$，$C(4,3)$.
(1) 画出$\triangle ABC$关于$x$轴对称的$\triangle A_1B_1C_1$，并写出点$A_1$，$B_1$的坐标；
(2) 画出$\triangle ABC$绕点$B$逆时针旋转$90^{\circ}$后的$\triangle A_2BC_2$；
(3) 求出(2)中线段$CC_2$所扫过的面积.(结果保留根号和$\pi$)
]

答案：

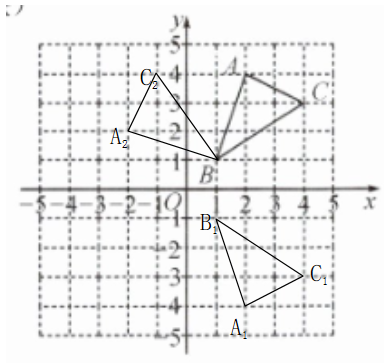
(1)，$A_{1}(2,-4)$，$B_{1}(1,-1)$.
(3)$BC=\sqrt{2^{2}+3^{2}}=\sqrt{13}$，$\therefore CC_{2}$扫过的面积为$\frac{90\pi×(\sqrt{13})^{2}}{360}=\frac{13\pi}{4}$.

13. (红河期末)如图，把$Rt\triangle ABC$的斜边$AB$放在定直线$l$上，按顺时针方向在$l$上转动两次，使它转到$\triangle A''B''C''$的位置. 设$BC = 2$，$AC = 2\sqrt{3}$，则顶点$A$运动到点$A''$的位置时，求点$A$经过的路线与直线$l$所围成的图形的面积.(结果保留$\pi$)
]

答案： 解:$\because$在$Rt\triangle ACB$中，$BC=2$，$AC=2\sqrt{3}$，$\therefore$由勾股定理，得$AB=4$.$\therefore AB=2BC$.$\therefore\angle CAB=30^{\circ}$，$\angle CBA=60^{\circ}$.$\therefore\angle ABA'=120^{\circ}$，$\angle A''C''A'=90^{\circ}$.$\therefore S=\frac{120\pi×4^{2}}{360}+\frac{90\pi×(2\sqrt{3})^{2}}{360}+\frac{1}{2}×2×2\sqrt{3}=\frac{25}{3}\pi+2\sqrt{3}$.

14. (昆明西山区一模)如图，冰淇淋蛋筒下部呈圆锥形，则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是 ( )

A.$27$ cm²
B.$54$ cm²
C.$27\pi$ cm²
D.$54\pi$ cm²

答案： C

15. (云南师大实验中学模拟)如图所示的是一个圆锥形状的生日帽. 若该圆锥形状帽子的母线长为 6 cm，底面半径为 2 cm，将该帽子沿母线剪开，则其侧面展开扇形的圆心角为________.
]

答案： 120°

16. (昆明官渡区期末)某同学用工具测一个圆锥形漏斗的尺寸，如图所示，由图中的数据可知圆锥形漏斗的侧面积为________cm².(结果保留$\pi$)

答案： 15π