第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
7. (昆明盘龙区期末)如图,在长为33m,宽为20m的矩形空地上修建同样宽的道路(阴影部分),余下的部分为草坪,草坪的面积为510m².若设道路的宽为x m,根据题意所列方程为(
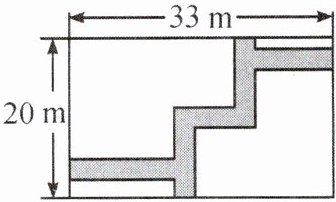
A.(20+x)(33−x)=510
B.(20−x)(33−x)=33×20−510
C.(20−x)(33−x)=510
D.(20+x)(33−x)=33×20−510
C
)
A.(20+x)(33−x)=510
B.(20−x)(33−x)=33×20−510
C.(20−x)(33−x)=510
D.(20+x)(33−x)=33×20−510
答案:
7.C
8. (教材9上P25复习题T8变式)(曲靖罗平县月考)某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30m的篱笆围成,已知墙长为18m.设这个苗圃园垂直于墙的一边的长为x m.
(1)用含x的代数式表示平行于墙的一边的长为
(2)当这个苗圃园的面积为88m²时,求x的值.
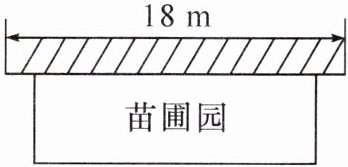
(1)用含x的代数式表示平行于墙的一边的长为
$(30-2x)$
m,x的取值范围为$6\leqslant x<15$
;(2)当这个苗圃园的面积为88m²时,求x的值.

答案:
8.解:
(1)$(30-2x)$ $6\leqslant x<15$
(2)根据题意,得$x(30-2x)=88$,解得$x_{1}=4$,$x_{2}=11$.$\because 6\leqslant x<15$,$\therefore x=4$不符合题意,舍去.$\therefore x$的值为11.
(1)$(30-2x)$ $6\leqslant x<15$
(2)根据题意,得$x(30-2x)=88$,解得$x_{1}=4$,$x_{2}=11$.$\because 6\leqslant x<15$,$\therefore x=4$不符合题意,舍去.$\therefore x$的值为11.
9. 已知一个包装盒的表面展开图如图.
(1)若此包装盒的容积为1125cm³,请列出关于x的方程,并求出x的值;
(2)是否存在这样的x的值,使得此包装盒的容积为1800cm³?若存在,请求出相应的x的值;若不存在,请说明理由.
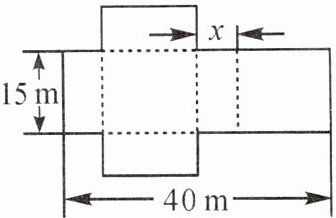
(1)若此包装盒的容积为1125cm³,请列出关于x的方程,并求出x的值;
(2)是否存在这样的x的值,使得此包装盒的容积为1800cm³?若存在,请求出相应的x的值;若不存在,请说明理由.

答案:
9.解:
(1)根据题意,得$15x(20-x)=1125$,整理,得$x^{2}-20x+75=0$.解得$x_{1}=5$,$x_{2}=15$.$\therefore x$的值为5或15.
(2)根据题意,得$15x(20-x)=1800$,即$x^{2}-20x+120=0$.$\because \Delta=(-20)^{2}-4×1×120=-80<0$,$\therefore$此方程无解,即不存在这样的$x$的值,使得包装盒的容积为$1800\ cm^{3}$.
(1)根据题意,得$15x(20-x)=1125$,整理,得$x^{2}-20x+75=0$.解得$x_{1}=5$,$x_{2}=15$.$\therefore x$的值为5或15.
(2)根据题意,得$15x(20-x)=1800$,即$x^{2}-20x+120=0$.$\because \Delta=(-20)^{2}-4×1×120=-80<0$,$\therefore$此方程无解,即不存在这样的$x$的值,使得包装盒的容积为$1800\ cm^{3}$.
10. 如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动.
(1)如果点P,Q分别从点A,B同时出发,那么几秒后,△PBQ的面积等于4cm²?
(2)如果点P,Q分别从点A,B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,△PBQ的面积能否等于7cm²?说明理由.

(1)如果点P,Q分别从点A,B同时出发,那么几秒后,△PBQ的面积等于4cm²?
(2)如果点P,Q分别从点A,B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,△PBQ的面积能否等于7cm²?说明理由.

答案:
10.解:
(1)设$x\ s$后,$\triangle PBQ$的面积等于$4\ cm^{2}$.根据题意,得$x(5-x)=4$,解得$x_{1}=1$,$x_{2}=4$.当$x=4$时,$2x=8>7$,不合题意,舍去.$\therefore x=1$.
答:$1\ s$后,$\triangle PBQ$的面积等于$4\ cm^{2}$.
(2)设$y\ s$后,$PQ=5\ cm$,则$(5-y)^{2}+(2y)^{2}=25$.解得$y_{1}=0$,$y_{2}=2$.
答:$0\ s$或$2\ s$后,$PQ$的长度等于$5\ cm$.
(3)不能,理由:根据题意,得$x(5-x)=7$.此方程无解.$\therefore \triangle PBQ$的面积不能等于$7\ cm^{2}$.
(1)设$x\ s$后,$\triangle PBQ$的面积等于$4\ cm^{2}$.根据题意,得$x(5-x)=4$,解得$x_{1}=1$,$x_{2}=4$.当$x=4$时,$2x=8>7$,不合题意,舍去.$\therefore x=1$.
答:$1\ s$后,$\triangle PBQ$的面积等于$4\ cm^{2}$.
(2)设$y\ s$后,$PQ=5\ cm$,则$(5-y)^{2}+(2y)^{2}=25$.解得$y_{1}=0$,$y_{2}=2$.
答:$0\ s$或$2\ s$后,$PQ$的长度等于$5\ cm$.
(3)不能,理由:根据题意,得$x(5-x)=7$.此方程无解.$\therefore \triangle PBQ$的面积不能等于$7\ cm^{2}$.
查看更多完整答案,请扫码查看


