《2025年名校课堂九年级数学全一册人教版云南专版》

7. （玉林中考）某小组做“用频率估计概率”的试验时，绘出的某一结果出现的频率折线图，则符合这一结果的试验可能是（ ）


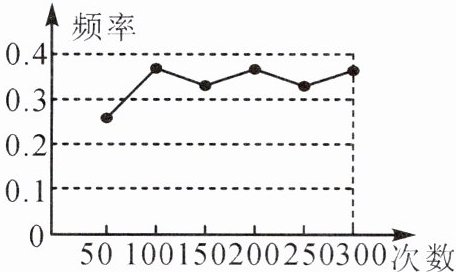
A.抛一枚硬币，出现正面朝上
B.掷一个正六面体的骰子，出现$3$点朝上
C.一副去掉大、小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃
D.从一个装有$2$个红球$1$个黑球的袋子中任取一球，取到的是黑球

答案： D

8. （昆明嵩明县期末）近几年，二维码逐渐进入了人们的生活，成为广大民众生活中不可或缺的一部分。小刚现将二维码打印在面积为$200cm^{2}$的正方形纸片上，如图。为了估计黑色阴影部分的面积，他在纸内随机掷点，经过大量实验，发现点落在黑色阴影的频率稳定在$0.6$左右，则据此估计此二维码中黑色阴影的面积为（ ）

A.$0.4cm^{2}$
B.$0.6cm^{2}$
C.$180cm^{2}$
D.$120cm^{2}$

答案： D

9. （教材$9$上$P148$习题$T5$变式）为了估计鱼池里有多少条鱼，先捕上$100$条作上记号，然后放回到鱼池里，过一段时间，待有记号的鱼完全混合鱼群后，再捕上$200$条鱼，发现其中带记号的鱼有$20$条，则可判断鱼池里大约有__________条鱼。

答案： 1 000

10. 某地区林业和草原局要考察一种树苗移植的成活率，对该地区这种树苗移植成活情况进行调查统计，并绘制了如图所示的统计图，根据统计图提供的信息解决下列问题：

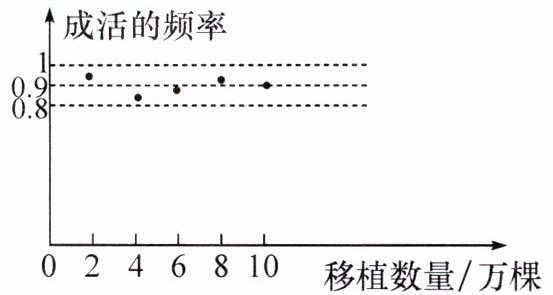
（1）这种树苗成活的频率稳定在________，成活的概率估计值为________；（结果精确到$0.1$）
（2）该地区已经移植这种树苗$5$万棵。
①估计这种树苗成活________万棵；
②如果该地区计划成活$18$万棵这种树苗，那么还需移植这种树苗约多少万棵？

答案： 解:
(1)0.9 0.9
(2)①4.5 ②18÷0.9-5=15(万棵).
答:该地区还需移植这种树苗约15万棵.

11. 小明和小亮两位同学做投掷骰子试验，他们共做了$100$次试验，试验的结果如下：

（1）计算“$2$点朝上”的频率和“$4$点朝上”的频率；
（2）小明说：“根据试验，一次试验中出现$3$点朝上的概率最大。”小亮说：“如果投掷$1000$次，那么出现$5$点朝上的次数正好是$200$次。”小明和小亮的说法正确吗？为什么？
（3）小明投掷一枚骰子，计算小明投掷点数不小于$3$的概率。

答案： 解:
(1)“2点朝上”的频率为$\frac{15}{100}=0.15$.“4点朝上”的频率为$\frac{16}{100}=0.16$.
(2)小明的说法错误,因为只有当试验的次数足够大时,该事件发生的频率才稳定在事件发生的概率附近.小亮的说法错误,因为事件的发生具有随机性.
(3)$P$(点数不小于3)=$\frac{4}{6}=\frac{2}{3}$.