《2025年名校课堂九年级数学全一册人教版云南专版》

8. 如图, 铁道口的栏杆短臂 $ OA $ 长 $ 1 \, m $, 长臂 $ OB $ 长 $ 8 \, m $. 当短臂外端 $ A $ 下降 $ 0.5 \, m $ 时, 长臂外端 $ B $ 升高 ( )

A.$ 2 \, m $
B.$ 4 \, m $
C.$ 4.5 \, m $
D.$ 8 \, m $

答案： B

9. 如图, 一条河的两岸有一段是平行的, 在河的南岸边每隔 $ 5 $ 米有一棵树, 在北岸边每隔 $ 60 $ 米有一根电线杆. 小丽站在离南岸边 $ 15 $ 米的点 $ P $ 处看北岸, 发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住, 并且在这两棵树之间还有三棵树, 则河宽为______米.

答案： 30

10. (昆明三中期中) 如图, $ A $, $ B $ 两点被池塘隔开, 在 $ AB $ 外任选一点 $ C $, 分别在 $ AC $, $ BC $ 上取点 $ D $, $ E $, 测得 $ CD = 20 \, m $, $ CE = 40 \, m $, $ AD = 100 \, m $, $ BE = 20 \, m $, 且 $ DE = 45 \, m $, 求 $ AB $ 的长.

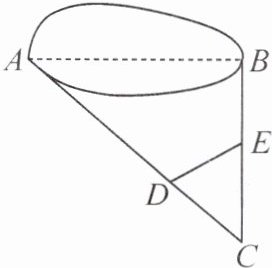
答案： 解:
∵CD=20m,CE=40m,AD=100m,BE=20m,
∴AC=CD+AD=120m,BC=CE+BE=60m.
∵$\frac{CE}{AC}=\frac{40}{120}=\frac{1}{3}$,$\frac{CD}{BC}=\frac{20}{60}=\frac{1}{3}$,
∴$\frac{CE}{AC}=\frac{CD}{BC}$.
∵∠C=∠C,
∴△CED∽△CAB.
∴$\frac{DE}{AB}=\frac{CD}{BC}=\frac{1}{3}$.
∴AB=3DE=135m.

11. (新考向 综合与实践 (教材 9 下 P58 复习题 T11 变式) 课本中有一道作业题:
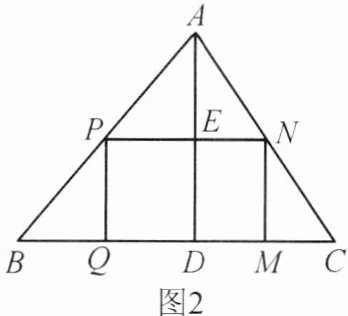
有一块三角形余料 $ ABC $, 它的边 $ BC = 120 \, mm $, 高 $ AD = 80 \, mm $. 要把它加工成正方形零件, 使正方形的一边在 $ BC $ 上, 其余两个顶点分别在 $ AB $, $ AC $ 上. 问加工成的正方形零件的边长是多少?
小颖解得此题的答案为 $ 48 \, mm $. 小颖善于反思, 她又提出了如下的问题.
(1) 如果原题中要加工的零件是一个矩形, 且此矩形是由两个并排放置的正方形所组成, 如图 1, 此时, 这个矩形零件的长和宽又分别为多少?
(2) 如果原题中所要加工的零件只是一个矩形, 如图 2, 这样, 此矩形零件的长和宽就不能确定, 但这个矩形的面积 $ S $ 有最大值, 求达到这个最大值时矩形零件的长和宽.

答案：
(1)设矩形的长PN=2y mm,则宽PQ=y mm.由条件可得,△APN∽△ABC,AD⊥PN,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,即$\frac{2y}{120}=\frac{80-y}{80}$,解得$y=\frac{240}{7}$.
∴$PN=\frac{240}{7}×2=\frac{480}{7}$(mm).
答:这个矩形零件的长和宽分别为$\frac{480}{7}$mm,$\frac{240}{7}$mm.
(2)设PN=x mm.由条件可得△APN∽△ABC,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,即$\frac{x}{120}=\frac{80-PQ}{80}$.
∴$PQ=80-\frac{2}{3}x$.
∴$S=PN\cdot PQ=x(80-\frac{2}{3}x)=-\frac{2}{3}x^{2}+80x=-\frac{2}{3}(x-60)^{2}+2400$.
∵$-\frac{2}{3}＜0$,
∴当x=60时,S的最大值为2400mm².此时PN=60mm,$PQ=80-\frac{2}{3}×60=40$(mm).