第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
9. (曲靖沾益区月考)如图,AB 是⊙O 的直径,CD 与⊙O 的相切,与 AB 的延长线相交于点 C. 若∠C = 26°,则∠A 的度数为( )
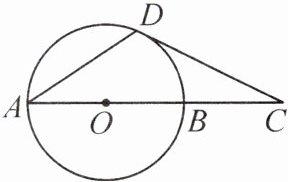
A.26°
B.27°
C.32°
D.37°

A.26°
B.27°
C.32°
D.37°
答案:
C
10. 新考向 真实情境 (玉溪模拟)为了落实“双减”政策,朝阳区一些学校在课后服务时段开设了与冬奥会项目冰壶有关的选修课. 如图,在冰壶比赛场地的一端画有一些同心圆作为营垒,其中有两个圆的半径分别约为 60 cm 和 180 cm,小明掷出一球恰好沿着小圆的切线滑行出界,则该球在大圆内滑行的路径 MN 的长度为____cm.
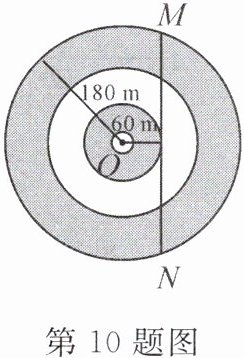

答案:
$240\sqrt{2}$
11. (昆明盘龙区期末)如图,AB 是⊙O 的直径,点 C 在⊙O 上,过点 C 的切线与 BA 的延长线相交于点 D,点 E 在$\widehat{BC}$上(不与点 B,C 重合),连接 BE,CE. 若∠D = 40°,则∠BEC =____.
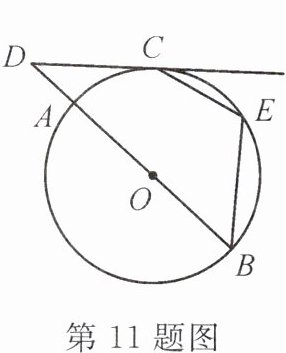

答案:
115°
12. (昆明官渡区期末)如图,⊙O 是△ABC 的外接圆,AB 是⊙O 的直径,D 是 AB 延长线上的一点,AE⊥CD 交 DC 的延长线于点 E,CF⊥AB 于点 F,且 CE = CF.
(1)判断直线 DE 与⊙O 的位置关系,并证明你的结论;
(2)若 AB = 6,BD = 3,求 AE 的长.
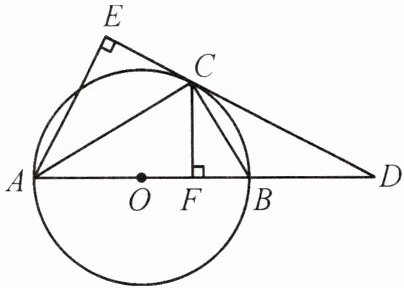
(1)判断直线 DE 与⊙O 的位置关系,并证明你的结论;
(2)若 AB = 6,BD = 3,求 AE 的长.

答案:
解:
(1)DE 与⊙O 相切.证明:连接 OC.
∵AE⊥CD,CF⊥AB,且 CE=CF,
∴∠EAC=∠BAC.
∵OA=OC,
∴∠BAC=∠ACO.
∴∠EAC=∠ACO.
∴OC//AE.
∴∠E=∠OCD=90°.
∴OC⊥DE.又
∵OC 是⊙O 的半径,
∴DE 与⊙O 相切.
(2)
∵AB=6,
∴OB=OC= $\frac{1}{2}$AB=3.
∴OD=OB+BD=6,OB=BD.又
∵∠OCD=90°,
∴BC= $\frac{1}{2}$OD=3.
∴BC=OB=OC.
∴△OBC 是等边三角形.
∴∠COB=60°.
∴∠D=30°.在 Rt△ADE 中,AD=AB+BD=9,
∴AE= $\frac{1}{2}$AD= $\frac{9}{2}$.
(1)DE 与⊙O 相切.证明:连接 OC.
∵AE⊥CD,CF⊥AB,且 CE=CF,
∴∠EAC=∠BAC.
∵OA=OC,
∴∠BAC=∠ACO.
∴∠EAC=∠ACO.
∴OC//AE.
∴∠E=∠OCD=90°.
∴OC⊥DE.又
∵OC 是⊙O 的半径,
∴DE 与⊙O 相切.
(2)
∵AB=6,
∴OB=OC= $\frac{1}{2}$AB=3.
∴OD=OB+BD=6,OB=BD.又
∵∠OCD=90°,
∴BC= $\frac{1}{2}$OD=3.
∴BC=OB=OC.
∴△OBC 是等边三角形.
∴∠COB=60°.
∴∠D=30°.在 Rt△ADE 中,AD=AB+BD=9,
∴AE= $\frac{1}{2}$AD= $\frac{9}{2}$.
13. 新考向 推理能力 (毕节中考)如图,在 Rt△ABC 中,∠ACB = 90°,以 AC 为直径作⊙O 交 AB 于点 D,连接 CD.
(1)求证:∠A = ∠BCD;
(2)若 M 为线段 BC 上一点,试问当点 M 在什么位置时,直线 DM 与⊙O 相切?并说明理由.
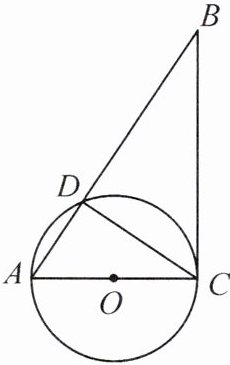
(1)求证:∠A = ∠BCD;
(2)若 M 为线段 BC 上一点,试问当点 M 在什么位置时,直线 DM 与⊙O 相切?并说明理由.

答案:
解:
(1)证明:
∵AC 为⊙O 的直径,
∴∠ADC=90°.
∴∠A+∠DCA=90°.
∵∠ACB=90°,
∴∠DCB+∠ACD=90°.
∴∠DCB=∠A.
(2)当 MC=MD(或点 M 是 BC 的中点)时,直线 DM 与⊙O 相切.理由:连接 DO.
∵DO=CO,
∴∠ODC=∠OCD.
∵DM=CM,
∴∠MCD=∠MDC.
∵∠DCO+∠MCD=90°,
∴∠ODC+∠MDC=90°.又
∵OD 为⊙O 的半径,
∴直线 DM 与⊙O 相切.
(1)证明:
∵AC 为⊙O 的直径,
∴∠ADC=90°.
∴∠A+∠DCA=90°.
∵∠ACB=90°,
∴∠DCB+∠ACD=90°.
∴∠DCB=∠A.
(2)当 MC=MD(或点 M 是 BC 的中点)时,直线 DM 与⊙O 相切.理由:连接 DO.
∵DO=CO,
∴∠ODC=∠OCD.
∵DM=CM,
∴∠MCD=∠MDC.
∵∠DCO+∠MCD=90°,
∴∠ODC+∠MDC=90°.又
∵OD 为⊙O 的半径,
∴直线 DM 与⊙O 相切.
查看更多完整答案,请扫码查看


