《2025年实验班提优训练八年级数学上册浙教版》

1.(教材 P7 例 1·变式)(2025·绍兴新昌期末)下列每组数分别是三根木棒的长度,能用它们摆成三角形的是(D).
A.4 cm,5 cm,10 cm
B.8 cm,7 cm,15 cm
C.6 cm,6 cm,13 cm
D.13 cm,12 cm,20 cm

答案： D [解析]A. 4+5＜10,不能摆成三角形,故A不符合题意;B. 8+7=15,不能摆成三角形,故B不符合题意;C. 6+6＜13,不能摆成三角形,故C不符合题意;D. 13+12＞20,能摆成三角形,故D符合题意.故选D.

2.(2025·宁波慈溪期末)如图,三角形有一部分被遮挡,我们可以判定此三角形的类型为(A).
A.钝角三角形
B.直角三角形
C.锐角三角形
D.不能确定

答案： A [解析]由题图知,三角形露出的部分为钝角,
∴我们可以判定此三角形的类型为钝角三角形.故选A.

3.(2025·龙泉庆阳期末)如图,小明在池塘一侧选取了一点 O,测得 OA= 16 m,OB= 12 m,则池塘两岸 A,B 间的距离可以是26m.(答案不唯一,写出一个即可)

答案： 26(答案不唯一) [解析]设A,B间的距离是x m,由三角形三边关系定理,得16-12＜x＜16+12,
∴4＜x＜28,
∴A,B间的距离可以是26 m(答案不唯一).

4.(2025·杭州拱墅区期末)在△ABC 中,∠A= 40°,∠B= 60°,则△ABC 是锐角三角形.(填入“锐角”“直角”“钝角”之一)

答案： 锐角 [解析]
∵∠A=40°,∠B=60°,
∴∠C=180°-∠A-∠B=180°-40°-60°=80°,即最大角∠C的度数＜90°,
∴△ABC是锐角三角形.

5.(2025·四川南充顺庆区期末)已知 a,b,c 是一个三角形的三条边长,则化简|a+b-c|-|b-a-c|的结果是多少？

答案：
∵a,b,c是一个三角形的三条边长,
∴a+b＞c,a+c＞b,
∴|a+b-c|-|b-a-c|=a+b-c-(a+c-b)=2b-2c.

6.(2025·杭州拱墅区期末)木工师傅要做一个三角形木架,有两根木条的长度为 7 cm 和 14 cm,第三根木条的长度可以是(B).
A.5 cm
B.18 cm
C.21 cm
D.23 cm

答案： B [解析]A. 7+5＜14,不能构成三角形,故A不符合题意;B. 7+14＞18,能构成三角形,故B符合题意;C. 7+14=21,不能构成三角形,故C不符合题意;D. 7+14＜23,不能构成三角形,故D不符合题意.故选B.

7.(2024·宁波鄞州区期末)若一个三角形的两边长分别为 3 和 6,则该三角形的周长可能是(B).
A.18
B.15
C.12
D.10

答案： B

8. 实验班原创 在△ABC 中,∠A-∠B= 30°,∠B-∠C= 30°,试判断△ABC 的形状.

答案： 根据题意,得∠A=∠B+30°,∠C=∠B-30°,
∴∠B+30°+∠B+∠B-30°=180°,解得∠B=60°,则∠A=60°+30°=90°,∠C=60°-30°=30°.故△ABC为直角三角形.

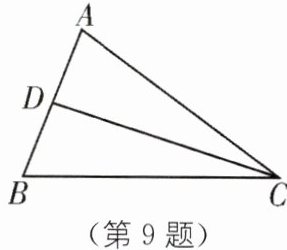
9. 如图,在△ABC 中,D 是边 BA 上一点,则AB+2CD＞AC+BC 成立吗？请说明理由.

答案： AB+2CD＞AC+BC成立.理由如下:在△ACD中,AD+CD＞AC,→三角形的任意两边之和大于第三边在△BCD中,BD+CD＞BC,两式相加,得(AD+BD)+2CD＞AC+BC,即AB+2CD＞AC+BC.