第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 传统文化 赵爽弦图 (2025·金华东阳期中)著名的赵爽弦图(如图(1),其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为$c^{2}$,也可以表示为$4×\frac{1}{2}ab+(a-b)^{2}$,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则$a^{2}+b^{2}= c^{2}$.
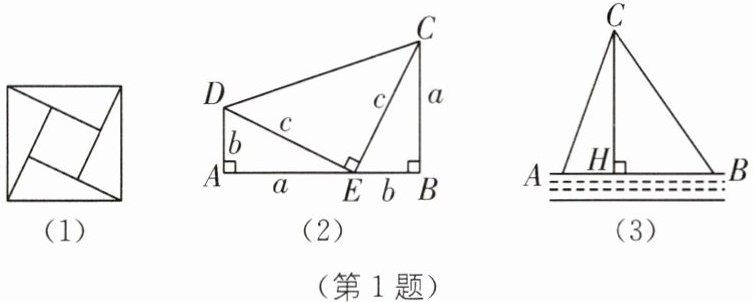
(1)图(2)为美国第二十任总统伽菲尔德的“总统证法”,请你利用图(2)推导勾股定理.
(2)如图(3),在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,$AB= AC$,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条路CH,且$CH\perp AB$.测得$CH= 0.8$千米,$HB= 0.4$千米,求新路CH比原路CA少多少千米?
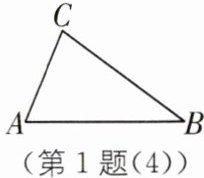
(3)如图(4),在$\triangle ABC$中,$AC= 10$,$BC= 17$,$AB= 21$,求$\triangle ABC$的面积.

(1)图(2)为美国第二十任总统伽菲尔德的“总统证法”,请你利用图(2)推导勾股定理.
(2)如图(3),在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,$AB= AC$,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条路CH,且$CH\perp AB$.测得$CH= 0.8$千米,$HB= 0.4$千米,求新路CH比原路CA少多少千米?
(3)如图(4),在$\triangle ABC$中,$AC= 10$,$BC= 17$,$AB= 21$,求$\triangle ABC$的面积.

答案:
1.
(1)梯形ABCD的面积可以表示为$\frac{1}{2}(a+b)(a+b)=\frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2},$也可以表示为$\frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2},$
∴$\frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2}=\frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2},$即a^{2}+b^{2}=c^{2}.
(2)设AC=AB=x千米,
∴AH=AB - BH=(x - 0.4)千米.
∵CA^{2}=CH^{2}+AH^{2},
∴x^{2}=0.8^{2}+(x -0.4)^{2},
∴x =1,即CA =1千米,
∴CA - CH=1 -0.8 =0.2(千米).故新路CH比原路CA少0.2千米.
(3)如图,过点C作$CH\perp AB,$垂足为H.设AH = y,
∴BH=AB - AH=21 - y,
∵$CH\perp AB,AB =21,AC =10,BC =17,$
∴CH^{2}=CA^{2}-AH^{2},CH^{2}=CB^{2}-BH^{2},
∴CA^{2}-AH^{2}=CB^{2}-BH^{2},即10^{2}-y^{2}=17^{2}-(21 - y)^{2},
∴y =6,
∴AH =6,
∴$CH=\sqrt{10^{2}-6^{2}}=8.$
∴$S_{\triangle ABC}=\frac{1}{2}×8×21 =84.$
1.
(1)梯形ABCD的面积可以表示为$\frac{1}{2}(a+b)(a+b)=\frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2},$也可以表示为$\frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2},$
∴$\frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2}=\frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2},$即a^{2}+b^{2}=c^{2}.
(2)设AC=AB=x千米,
∴AH=AB - BH=(x - 0.4)千米.
∵CA^{2}=CH^{2}+AH^{2},
∴x^{2}=0.8^{2}+(x -0.4)^{2},
∴x =1,即CA =1千米,
∴CA - CH=1 -0.8 =0.2(千米).故新路CH比原路CA少0.2千米.
(3)如图,过点C作$CH\perp AB,$垂足为H.设AH = y,
∴BH=AB - AH=21 - y,
∵$CH\perp AB,AB =21,AC =10,BC =17,$
∴CH^{2}=CA^{2}-AH^{2},CH^{2}=CB^{2}-BH^{2},
∴CA^{2}-AH^{2}=CB^{2}-BH^{2},即10^{2}-y^{2}=17^{2}-(21 - y)^{2},
∴y =6,
∴AH =6,
∴$CH=\sqrt{10^{2}-6^{2}}=8.$
∴$S_{\triangle ABC}=\frac{1}{2}×8×21 =84.$

2. (四川成都石室中学自主招生)地震是人类一直在研究并试图战胜的自然灾害,四川是地震频发区,为更好地研究地震的破坏性,石室中学创新基地的同学做了如下模拟监测实验.如图为地面(AB)以下至地震波反射面(MN)的横截面示意图,其中,O为震源,A为震中,B为观测站,$OA\perp AB$,$AB// MN$.从O会同时发出两种震波:直达波(路径为OB)和反射波(路径为OCB),它们的传播速度相同.已知震源深度$h= 14$km,震中至观测站距离$AB= 48$km.
(1)求直达波传播的距离OB;
(2)已知反射波(路径OCB)满足$\angle OCM= \angle BCN$,地震波的传播速度为5km/s,观测站收到两种地震波的时间差为2s,求地面与反射面的距离l.
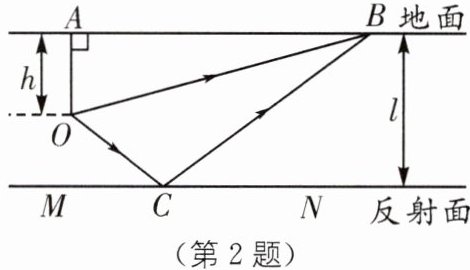
(1)求直达波传播的距离OB;
(2)已知反射波(路径OCB)满足$\angle OCM= \angle BCN$,地震波的传播速度为5km/s,观测站收到两种地震波的时间差为2s,求地面与反射面的距离l.

答案:
2.
(1)
∵$OA\perp AB$,
∴$\angle OAB =90^{\circ}$,
∵$OA = h =14$km,$AB =48$km,
∴$OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{14^{2}+48^{2}}=50$(km).
(2)延长AO交MN于点P,延长BC交AO的延长线于点Q.
∵直达波和反射波传播速度相同,地震波速度$ =5$km/s,观测站收到两种地震波的时间差为2s,
∴$\frac{OC + BC}{5}-\frac{OB}{5}=2$.
∵$OB =50$km,
∴$OC + BC =60$km.
∵$\angle OCM=\angle BCN$,$\angle BCN=\angle PCQ$,
∴$\angle OCM=\angle PCQ$.
∵$CP\perp OQ$,
∴$OC = QC$,
∴$OP = PQ$,
∴$QB = QC + CB = OC + CB =60$km.在Rt△AQB中,$AQ^{2}+AB^{2}=QB^{2}$.
∵$AB =48$km,$QB =60$km,解得$AQ =36$km,
∴$OQ = AQ - OA =22$(km),
∴$OP =11$km,
∴$l = AP = AO + OP =14 +11 =25$(km).
(1)
∵$OA\perp AB$,
∴$\angle OAB =90^{\circ}$,
∵$OA = h =14$km,$AB =48$km,
∴$OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{14^{2}+48^{2}}=50$(km).
(2)延长AO交MN于点P,延长BC交AO的延长线于点Q.
∵直达波和反射波传播速度相同,地震波速度$ =5$km/s,观测站收到两种地震波的时间差为2s,
∴$\frac{OC + BC}{5}-\frac{OB}{5}=2$.
∵$OB =50$km,
∴$OC + BC =60$km.
∵$\angle OCM=\angle BCN$,$\angle BCN=\angle PCQ$,
∴$\angle OCM=\angle PCQ$.
∵$CP\perp OQ$,
∴$OC = QC$,
∴$OP = PQ$,
∴$QB = QC + CB = OC + CB =60$km.在Rt△AQB中,$AQ^{2}+AB^{2}=QB^{2}$.
∵$AB =48$km,$QB =60$km,解得$AQ =36$km,
∴$OQ = AQ - OA =22$(km),
∴$OP =11$km,
∴$l = AP = AO + OP =14 +11 =25$(km).
3. 如图,将长方形ABCD沿AF折叠,使点B落在DC边的点E处,已知$AB= 15$cm,$BC= 12$cm,求FC的长.
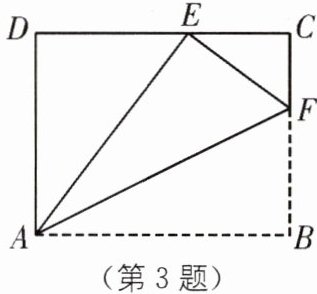

答案:
3. 在Rt△ADE中,$\angle D =90^{\circ}$,$AD = BC =12$cm,$AE = AB =15$cm,$DE^{2}=AE^{2}-AD^{2}$,
∴$DE=\sqrt{AE^{2}-AD^{2}}=\sqrt{15^{2}-12^{2}}=9$(cm).
∴$EC = DC - DE =15 -9 =6$(cm).设$FC = x$cm,则$FB = EF=(12 - x)$cm,在Rt△EFC中,$EF^{2}=EC^{2}+FC^{2}$,即$(12 - x)^{2}=6^{2}+x^{2}$,解得$x =4.5$,
∴$FC$的长为$4.5$cm.
∴$DE=\sqrt{AE^{2}-AD^{2}}=\sqrt{15^{2}-12^{2}}=9$(cm).
∴$EC = DC - DE =15 -9 =6$(cm).设$FC = x$cm,则$FB = EF=(12 - x)$cm,在Rt△EFC中,$EF^{2}=EC^{2}+FC^{2}$,即$(12 - x)^{2}=6^{2}+x^{2}$,解得$x =4.5$,
∴$FC$的长为$4.5$cm.
查看更多完整答案,请扫码查看


