第127页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 教材 P169 例 3·变式 一次函数 $ y= kx+b(k \neq 0) $,当 $ x= 1 $ 时,$ y= 1 $;当 $ x= 2 $ 时,$ y= -4 $,则 $ k $ 与 $ b $ 的值为(
A.$ \begin{cases} k= 3, \\ b= -2 \end{cases} $
B.$ \begin{cases} k= -3, \\ b= 4 \end{cases} $
C.$ \begin{cases} k= -5, \\ b= 6 \end{cases} $
D.$ \begin{cases} k= 6, \\ b= -5 \end{cases} $
C
).A.$ \begin{cases} k= 3, \\ b= -2 \end{cases} $
B.$ \begin{cases} k= -3, \\ b= 4 \end{cases} $
C.$ \begin{cases} k= -5, \\ b= 6 \end{cases} $
D.$ \begin{cases} k= 6, \\ b= -5 \end{cases} $
答案:
C [解析]把x=1,y=1和x=2,y=-4代入y=kx+b,得{k+b=1,2k+b=-4,解得{k=-5,b=6.故选C.
2. (2025·湖南株洲醴陵期末)小红在练习仰卧起坐,本月 1 日至 4 日的成绩与日期具有如下关系:
| 日期 $ x $/日 | 1 | 2 | 3 | 4 |
| 成绩 $ y $/个 | 40 | 43 | 46 | 49 |

小红的仰卧起坐成绩 $ y $ 与日期 $ x $ 之间近似为一次函数关系,则该一次函数表达式为______
| 日期 $ x $/日 | 1 | 2 | 3 | 4 |
| 成绩 $ y $/个 | 40 | 43 | 46 | 49 |

小红的仰卧起坐成绩 $ y $ 与日期 $ x $ 之间近似为一次函数关系,则该一次函数表达式为______
y=3x+37
.
答案:
y=3x+37
3. 跨学科 沸点 (2024·安康汉滨区一模)某兴趣小组通过实验估算某液体的沸点,经过测量,气压为标准大气压,并得到几组对应的数据如下:
| 加热时间 $ t $/s | 0 | 10 | 20 | 30 |
| 液体温度 $ y/^\circ \text{C} $ | 8 | 18 | 28 | 38 |
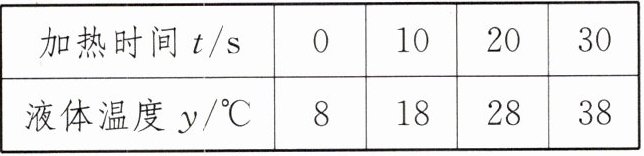
(1)兴趣小组发现液体沸腾前,液体温度与加热时间之间满足一次函数关系,求 $ y $ 与 $ t $ 之间的函数表达式;
(2)当加热 3 min 时该液体沸腾,求该液体的沸点.
| 加热时间 $ t $/s | 0 | 10 | 20 | 30 |
| 液体温度 $ y/^\circ \text{C} $ | 8 | 18 | 28 | 38 |

(1)兴趣小组发现液体沸腾前,液体温度与加热时间之间满足一次函数关系,求 $ y $ 与 $ t $ 之间的函数表达式;
(2)当加热 3 min 时该液体沸腾,求该液体的沸点.
答案:
(1)设y与t之间的函数表达式为y=kt+b(k,b为常数,且k≠0),将t=0,y=8和t=10,y=18代入y=kt+b,得{b=8,10k+b=18,解得{k=1,b=8,
∴y=t+8.
(2)3×60=180(s).当t=180时,y=180+8=188,
∴该液体的沸点是188℃.
(1)设y与t之间的函数表达式为y=kt+b(k,b为常数,且k≠0),将t=0,y=8和t=10,y=18代入y=kt+b,得{b=8,10k+b=18,解得{k=1,b=8,
∴y=t+8.
(2)3×60=180(s).当t=180时,y=180+8=188,
∴该液体的沸点是188℃.
4. “五一节”期间,乐乐老师一家自驾游去了离家 260 千米的某目的地,下面是她们离家的距离 $ y $(千米)与汽车行驶时间 $ x $(小时)之间的函数图象,当她们出发 2.3 小时时,离目的地还有(
A.48 千米
B.32 千米
C.28 千米
D.22 千米
D
).A.48 千米
B.32 千米
C.28 千米
D.22 千米
答案:
D [解析]由题知,当1.5≤x≤2.5时,设y=kx+b,则{1.5k+b=150,2.5k+b=260,解得{k=110,b=-15,所以y=110x-15.将x=2.3代入y=110x-15,得y=110×2.3-15=238,所以他们离目的地的距离为260-238=22(千米).故选D.
5. 传统文化 杆秤 (2025·朔州怀仁一模)杆秤是利用杠杆原理来称物品质量的简易衡器,其秤砣到秤纽的水平距离 $ y $ cm 与所挂物重 $ x $ kg 之间满足一次函数关系,如下为记录几次数据之后所列表格:
| $ x $/kg | 1 | 2 | 3 |
| $ y $/cm | 8 | 13.5 | 19 |
则 $ y $ 与 $ x $ 之间的关系式为( ).
A.$ y= 5.5x+2.5 $
B.$ y= 5.5x-2.5 $
C.$ y= 11x+8 $
D.$ y= 11x $
| $ x $/kg | 1 | 2 | 3 |
| $ y $/cm | 8 | 13.5 | 19 |
则 $ y $ 与 $ x $ 之间的关系式为( ).
A.$ y= 5.5x+2.5 $
B.$ y= 5.5x-2.5 $
C.$ y= 11x+8 $
D.$ y= 11x $
答案:
5. A
6. 跨学科 温度 (2025·福建厦门大同中学期中)摄氏温度与华氏温度是两大国际主流的计量温度的单位. 摄氏温度与华氏温度部分对应如下表所示:
| 摄氏温度 | 0 | 10 | 20 | 30 | 40 | … |
| 华氏温度 | 32 | 50 | 68 | 86 | 104 | … |
若摄氏温度为 $ m $,华氏温度为 $ n $,则把摄氏温度转换为华氏温度的关系式为______.
| 摄氏温度 | 0 | 10 | 20 | 30 | 40 | … |
| 华氏温度 | 32 | 50 | 68 | 86 | 104 | … |
若摄氏温度为 $ m $,华氏温度为 $ n $,则把摄氏温度转换为华氏温度的关系式为______.
答案:
6. n=1.8m+32 [解析]设n=km+b,将m=0,n=32和m=10,n=50代入n=km+b,得{b=32,10k+b=50,解得{k=1.8,b=32,所以把摄氏温度转换为华氏温度的关系式为n=1.8m+32
7. (2024·湖州长兴期末)已知 $ \triangle ABC $ 的顶点坐标分别为 $ A(-5,0) $,$ B(3,0) $,$ C(0,3) $,当过点 $ C $ 的直线 $ l $ 将 $ \triangle ABC $ 分成面积相等的两部分时,直线 $ l $ 所表示的函数表达式为______.
答案:
7. y=3x+3 [解析]由题意,得线段AB的中点坐标为(-1,0),设直线l的函数表达式为y=kx+b,则{b=3,-k+b=0,解得{k=3,b=3,
∴直线l的函数表达式为y=3x+3
∴直线l的函数表达式为y=3x+3
查看更多完整答案,请扫码查看


