《2025年实验班提优训练八年级数学上册浙教版》

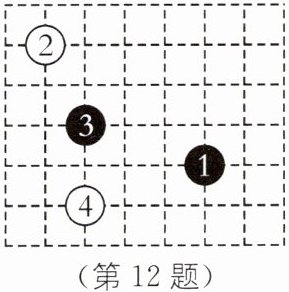
12.(2024·陕西咸阳武功期末)围棋起源于中国,它蕴含着中华文化的丰富内涵,是中国文化与文明的体现.如图,围棋盘放在某个平面直角坐标系内,黑棋①的坐标为(-1,-2),白棋④的坐标为(-4,-3),则白棋②的坐标为______(−5,1).

答案： 12.(−5,1)

13.(2024·哈尔滨道外区一模)如图,把边长为1的等边三角形从原点出发沿x轴正半轴方向移动,$A_1(1,0)$,$A_2(1,0)$,$A_3(2\frac{1}{2},\frac{\sqrt{3}}{2})$,…,则$A_7$的坐标为______.

答案：
13.(7,0)　[解析]如图所示， 发现$A_{3},A_{6}$的纵坐标是相等的，$A_{1},A_{4}$的纵坐标是相等的，
∴$A_{7}$的纵坐标与$A_{1},A_{4}$是相等的，且为0.
∵三角形是边长为1的等边三角形,由图,得$A_{1},A_{4}$的横坐标相差为3,
∴$A_{4},A_{7}$的横坐标相差为3,即$A_{7}$的横坐标为1+3+3=7,
∴$A_{7}$的坐标为(7,0).

14.(2024·丽水松阳期末)已知实数x,y,t,满足x= 1+t,y= 1-t.
(1)当x= 3时,求y的值；
(2)若点(x,y)在第四象限,求t的取值范围；
(3)在(2)的条件下,求证：$x^2 - y^2 - x - y - 2＞0$.

答案： 14.
(1)
∵x=1+t=3,
∴t=2.把t=2代入y=1−t,得y=1−2=−1.
(2)
∵点(x,y)在第四象限,
∴x=1+t＞0,y=1−t＜0,解得t＞−1,t＞1,
∴t＞1.
(3)
∵x=1+t,y=1−t,
∴x=2−y,
∴$x^{2}-y^{2}-x-y-2=(2-y)^{2}-y^{2}-(2-y)-y-2=-4y$.
∵y＜0,
∴-4y＞0,即$x^{2}-y^{2}-x-y-2＞0$. 一题多解
∵x=1+t,y=1−t,
∴$x^{2}-y^{2}-x-y-2=(1+t)^{2}-(1-t)^{2}-(1+t)-(1-t)-2=4(t-1)$.
∵t＞1,
∴t−1＞0,
∴4(t−1)＞0,即$x^{2}-y^{2}-x-y-2＞0$.

15.(2024·广西崇左江州区期末)已知当m,n都是实数,且满足2m= 8+n时,称$p(m-1,\frac{n+2}{2})$为“开心点”.例如点A(5,3)为“开心点”.
∵当A(5,3)时,$m-1= 5$,$\frac{n+2}{2}= 3$,得m= 6,n= 4,
∴2m= 2×6= 12,8+n= 8+4= 12,
∴2m= 8+n,∴A(5,3)是“开心点”.
(1)判断点B(9,6)是否为“开心点”,并说明理由.
(2)若点M(a,2a-3)是“开心点”,请判断点M在第几象限？并说明理由.

答案： 15.
(1)点B(9,6)不是“开心点”.理由如下:
∵当点B(9,6)时,m−1=9,$\frac{n+2}{2}$=6,解得m=10,n=10.
∵2m=20,8+n=18,
∴2m≠8+n,
∴点B(9,6)不是“开心点”
(2)点M在第四象限.理由如下:
∵点M(a,2a−3)是“开心点”,
∴m−1=a,$\frac{n+2}{2}$=2a−3,解得m=a+1,n=4a−8.
∵2m=8+n,
∴2(a+1)=8+4a−8,解得a=1,
∴2a−3=−1,此时点M的坐标为(1,−1),
∴点M在第四象限.

16. 已知$A_1(2,1)$,$A_2(-1,0)$,…,$A_k(x_k,y_k)$(k为正整数),且满足$x_k= \frac{1}{1-x_{k-1}}$,$y_k= 1-y_{k-1}$,求$A_{2025}$的坐标.

答案： 16.
∵$A_{1}(2,1)$，$A_{2}(-1,0)$，…，$A_{k}(x_{k},y_{k})$（k为正整数），且满足$x_{k}=\frac {1}{1-x_{k-1}}$，$y_{k}=1-y_{k-1}$，
∴$A_{3}(\frac {1}{2},1)$，$A_{4}(2,0)$，$A_{5}(-1,1)$，$A_{6}(\frac {1}{2},0)$，$A_{7}(2,1)$，$A_{8}(-1,0)$. 通过以上几个点的坐标可以发现规律，这些点每6个为一个循环.
∵2025÷6=337……3，
∴$A_{2025}$的坐标为$(\frac {1}{2},1)$.