《2025年实验班提优训练八年级数学上册浙教版》

1.(2025.龙泉庆阳期末)下列函数中,是一次函数的为(A).
A.y= 2x-1
B.y= $\frac{500}{x}$
C.y= x(50-x)
D.y= 2

答案： A

2.(2025.绍兴诸暨期末)已知函数y= 2x+2m-2是正比例函数,则m= 1.

答案： 1

3. 下列函数中,哪些是一
次函数？若是一次函数,写出系数k和常数项b的值.
(1)y= -5x+12; (2)y= 4(7-x);
(3)y= 16x; (4)S= x(6-x).

答案：
(1)根据一次函数的定义,$y=-5x+12$是一次函数,其中$k=-5$,$b=12$.
(2)$y=4(7-x)=-4x+28$,根据一次函数的定义,$y=-4x+28$是一次函数,其中$k=-4$,$b=28$.
(3)根据一次函数的定义,$y=16x$是一次函数,其中$k=16$,$b=0$.
(4)$\because S=x(6-x)=6x-x^{2}$,自变量的次数不是1,$\therefore S=x(6-x)=6x-x^{2}$不符合一次函数的定义,故不是一次函数.

4.已知$y= (m-1)x^2-$|ml+n+4.
(1)当m,n取何值时,y是x的一次函数?
(2)当m,n取何值时,y是x的正比例函数?

答案：
(1)根据一次函数的定义,得$m-1≠0$且$2-|m|=1$,解得$m=-1$,$\therefore$当$m=-1$,$n$为任意实数时,$y$是$x$的一次函数.
(2)根据正比例函数的定义,得$m-1≠0$且$2-|m|=1$,$n+4=0$,解得$m=-1$,$n=-4$,$\therefore$当$m=-1$,$n=-4$时,$y$是$x$的正比例函数.

5.(2024.上海杨浦区期末)下面各组变量的关系中,成正比例关系的有(D).
A.人的身高与年龄
B.汽车从甲地到乙地,所用时间与行驶速度
C.正方形的面积与它的边长
D.圆的周长与它的半径

答案： D

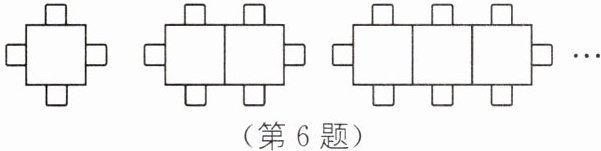
6.学校食堂按如图方式摆放餐桌和椅子.若用
x表示餐桌的张数,y表示椅子的把数,请你
写出椅子数y(把)与餐桌数x(张)之间的函
数关系式______$y=2x+2$.

答案： $y=2x+2$ [解析] 观察图形:当$x=1$时,$y=4$;当$x=2$时,$y=6$;当$x=3$时,$y=8$;$\cdots$,可见每增加一张桌子,便增加2个座位,$\therefore x$张餐桌共有$(2x+2)$个座位,$\therefore$可坐人数$y=2x+2$.故$y$与$x$之间的函数关系式为$y=2x+2$.

7.跨学科声音传播](2024.江苏宿迁宿豫区期末)声音在常温空气中的传播速度是340m/s,则传播距离l(m)与传播时间t(s)之间的函数表达式为$l=340t$.

答案： $l=340t$

8.(2025.山东烟台莱州期末)已知函数y= (m-1)x +$m^2-1$是正比例函数,则m=-1.

答案： -1 [解析] 由正比例函数的定义,可得$m^{2}-1=0$,且$m-1≠0$,解得$m=-1$.

9.实验班原创在$y= (k-2)x+k^2-4$中,若y是关于x的正比例函数,则k的值为-2;若y是关于x的一次函数,则k的取值范围是$k≠2$.

答案： -2 $k≠2$ [解析] 若$y$是关于$x$的正比例函数,则$k-2≠0$且$k^{2}-4=0$,解得$k≠2$,且$k=±2$,$\therefore k=-2$.若$y$是关于$x$的一次函数,则$k-2≠0$,解得$k≠2$.

10.中考新考法新定义问题新定义:[a,b]为一次函数y= ax十b(a≠0,a,b为实数)的“关联数”.若“关联数"为[3,m-2]的一次函数是正比例函数,则点(1-m,1+m)在第二象限.

答案： 二

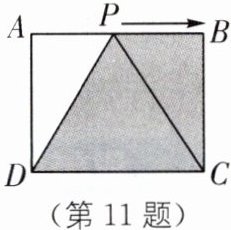
11.分类讨论思想如图,在长方形ABCD中,BC=
12cm,DC= 15cm,点P从点A开始以
1cm/s的速度向点B运动,设点P运动的时
间为t(s),阴影部分的面积为$S(cm^2).$
(1)求阴影部分的面积S关于t的函数表达式以及自变量t的取值范围;
(2)当△DCP为等腰三角形时,求阴影部分的面积.

答案：
(1)由题意,得$AP=t\ \text{cm}$,则$PB=(15-t)\ \text{cm}$,$\therefore S=\frac{1}{2}(PB+DC)\cdot BC=\frac{1}{2}(15-t+15)×12=-6t+180(0\leqslant t\leqslant15)$.故阴影部分的面积$S$关于$t$的函数表达式为$S=-6t+180(0\leqslant t\leqslant15)$.
(2)当$\triangle DCP$为等腰三角形时,分三种情况:
①当$PD=PC$时,$P$为$AB$的中点,此时$t=\frac{15}{2}\ \text{s}$,$\therefore S=-6×\frac{15}{2}+180=135(\text{cm}^{2})$;
②当$CD=CP$时,在$\text{Rt}\triangle PBC$中,$PB=\sqrt{CP^{2}-BC^{2}}=\sqrt{CD^{2}-BC^{2}}=\sqrt{15^{2}-12^{2}}=9(\text{cm})$,$\therefore t=AP=15-9=6(\text{s})$,$\therefore S=-6×6+180=144(\text{cm}^{2})$;
③当$PD=DC$时,在$\text{Rt}\triangle ADP$中,$AP=\sqrt{PD^{2}-AD^{2}}=\sqrt{DC^{2}-BC^{2}}=\sqrt{15^{2}-12^{2}}=9(\text{cm})$,$\therefore t=9(\text{s})$,$\therefore S=-6×9+180=126(\text{cm}^{2})$.综上所述,当$\triangle DCP$为等腰三角形时,阴影部分的面积为$135\ \text{cm}^{2}$或$144\ \text{cm}^{2}$或$126\ \text{cm}^{2}$.