《2025年实验班提优训练八年级数学上册浙教版》

1. 实验班原创 在平面直角坐标系中,将点 P(-2,-4)向右平移 3 个单位长度后得到的点所在的位置是(D).
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： D [解析]根据平移规律，横坐标右移加，左移减；纵坐标上移加，下移减即可得到答案。将点P(-2,-4)向右平移3个单位长度后得到的点的坐标为(-2+3,-4)，即(1,-4)，位于第四象限。故选D。

2. (2024·绍兴一模)在平面直角坐标系中,将点 P(-3,-2)水平向右平移 a 个单位后落在第四象限内,则 a 的值可以是4.(写出一个即可)

答案： 4(答案不唯一)　[解析]第四象限的点的特征为(+,-)，只要平移后横坐标为正即可。

3. (2024·金华东阳期末)将点 P(-2,-3)向右平移 3 个单位长度,再向上平移 2 个单位长度得到点 Q,则点 Q 的坐标是(1,-1).

答案： (1,-1)

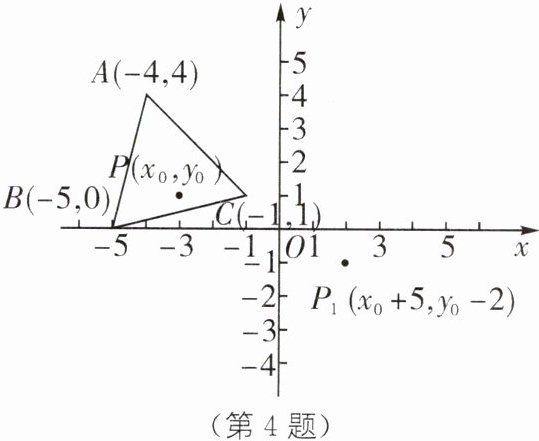
4. 教材 P142 作业题 T4·变式 如图,△ABC 内任意一点 P(x₀,y₀)经平移后对应的点为$ P_1(x₀+5,y₀-2),$将△ABC 作同样的平移得到$△A_1B_1C_1,$求点$ A_1,B_1,C_1 $的坐标,并画出$△A_1B_1C_1.$

答案：
由点P(x₀,y₀)平移到点P₁(x₀+5,y₀-2)，得点A(-4,4)平移到点A₁(1,2)，点B(-5,0)平移到点B₁(0,-2)，点C(-1,1)平移到点C₁(4,-1)。在平面直角坐标系中描出A₁,B₁,C₁三点，顺次连结这三个点，即可得到△A₁B₁C₁，如图所示。　　　　

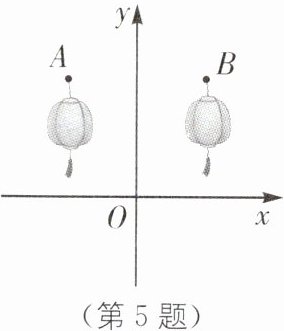
5. 传统文化 春节习俗 (2024·杭州萧山区二模)春节是中华民族的传统节日,古人常用写“桃符”的方式来祈福避祸,而现在,人们常用贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿.如图,在平面直角坐标系中,A,B 两处灯笼的位置关于 y 轴对称,若点 A 的坐标为(-2,4),则点 B 的坐标为(B).

A.(4,2)
B.(2,4)
C.(-2,4)
D.(-2,-4)

答案： B

6. (2025·安徽合肥四十五中期中)如图,在平面直角坐标系中有若干个整数点,其顺序按图中“→”方向排列,依次为(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1),…,根据这个规律,可得第 55 个点的坐标为(C).
A.(10,0)
B.(10,1)
C.(10,5)
D.(10,4)

答案： C　[解析]在横坐标上，第一列有一个点，第二列有2个点，…，第n个有n个点，并且奇数列点数对称而偶数列点数y轴上方比下方多一个。
∵1+2+3+…+10=55，
∴第55个点是第10列最上面一个数。
∵第10列有10个数，y轴上方比下方多一个，
∴x轴上方有5个，x轴上有1个，x轴下方有4个。
∵x轴上的点的坐标为(10,0)，
∴最上面的点的坐标为(10,5)。故选C

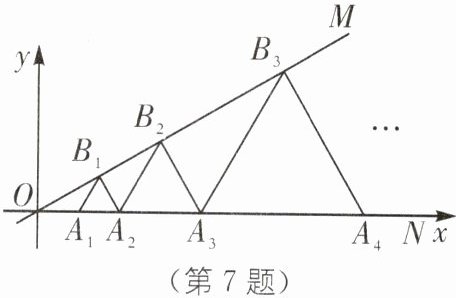
7. (2025·宁波江北区青藤书院月考)如图,在平面直角坐标系中,O 为坐标原点,点 N 在 x 轴正半轴上,点$ A_1,A_2,A_3,…,$在射线 ON 上,点$ B_1,B_2,B_3,…$在射线 OM 上$,∠MON= 30°,△A_1B_1A_2,△A_2B_2A_3,△A_3B_3A_4,…,$均为等边三角形,以此类推,若$ OA_1= 1,$则$ B_2₀_2_4 $的横坐标为______3×2²⁰²².

答案： 3×2²⁰²²　[解析]过点B₁作B₁C⊥x轴于点C。
∵△A₁B₁A₂是等边三角形，
∴∠A₂A₁B₁=60°，
∴∠OB₁A₁=30°=∠A₁OB₁，
∴A₁B₁=OA₁=1，A₁A₂=A₁B₁=1，
∴A₁C= $\frac{1}{2}$A₁A₂= $\frac{1}{2}$，
∴OC=OA₁+A₁C= $\frac{3}{2}$，即点B₁的横坐标为 $\frac{3}{2}$，　同理，可得点B₂的横坐标为2×$\frac{3}{2}$，　点B₃的横坐标为2²×$\frac{3}{2}$，点B₄的横坐标为2³×$\frac{3}{2}$，点B₅的横坐标为2⁴×$\frac{3}{2}$，点B₆的横坐标为2⁵×$\frac{3}{2}$，点B₇的横坐标为2⁶×$\frac{3}{2}$，…，　归纳类推，得点Bₙ的横坐标为2ⁿ⁻¹×$\frac{3}{2}$=3×2ⁿ⁻²(n为正整数)，则点B₂₀₂₄的横坐标为3×2²⁰²⁴⁻²=3×2²⁰²²。

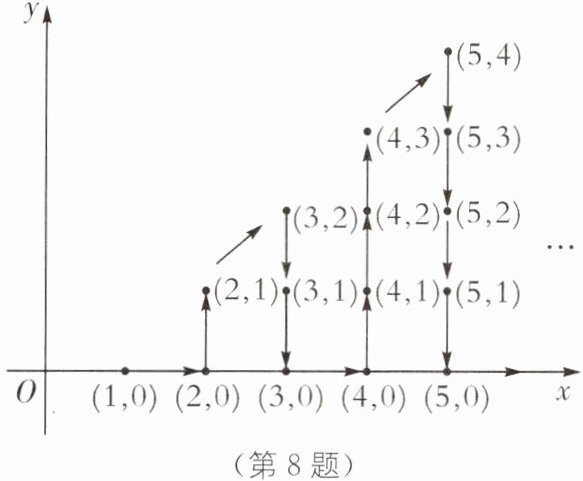
8. 中考新考法 探索规律 (2025·山东淄博高新区期末)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),根据这个规律探索可得第 2025 个点的坐标是______(64,8).

答案： (64,8)　[解析]把第一个点(1,0)作为第一列，(2,0)，(2,1)作为第二列，以此类推，则第一列有一个数，第二列有2个数，…，第n列有n个数，则n列共有$\frac{n(n+1)}{2}$个数，并且在奇数列点的顺序是由上到下，偶数列点的顺序由下到上。　因为1+2+3+…+63=2016，所以第2025个点一定在第64列，由下到上是第9个数，　所以第2025个点的坐标是(64,8)。