第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 新情境 数学与生活融合 (2024·江苏南京秦淮区期中)
如图,某同学在课桌上随意将一块三角板叠放在直尺上,则∠1+∠2 等于( ).
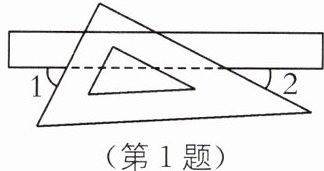
A.60°
B.90°
C.75°
D.105°
如图,某同学在课桌上随意将一块三角板叠放在直尺上,则∠1+∠2 等于( ).

A.60°
B.90°
C.75°
D.105°
答案:
B [解析] 如图所示.

∵∠1与∠4是对顶角,∠2与∠3是对顶角,
∴∠1=∠4,∠2=∠3.
∵此三角形是直角三角形,
∴∠3+∠4=90°,即∠1+∠2=90°. 故选 B.
B [解析] 如图所示.

∵∠1与∠4是对顶角,∠2与∠3是对顶角,
∴∠1=∠4,∠2=∠3.
∵此三角形是直角三角形,
∴∠3+∠4=90°,即∠1+∠2=90°. 故选 B.
2. 8字模型 如图,在△ABC 中,点 D,G 分别在边 BC,AC 上,且∠B= ∠GDC,F 在 DG 的延长线上,E 在 GC 上,如果∠AGF= ∠DAG+∠3,试说明∠1= ∠3.
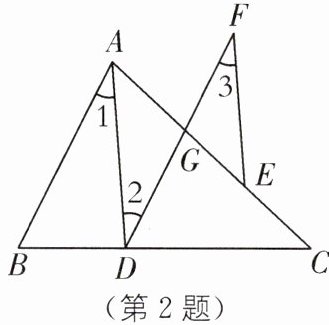

答案:
∵∠B=∠GDC(已知),
∴AB//GD(同位角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等).
∵∠AGF=180°-∠AGD=180°-(180°-∠2-∠DAG)=∠2+∠DAG(三角形内角和定理),∠AGF=∠DAG+∠3(已知),
∴∠2=∠3(等式性质),
∴∠1=∠3(等量代换).
∵∠B=∠GDC(已知),
∴AB//GD(同位角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等).
∵∠AGF=180°-∠AGD=180°-(180°-∠2-∠DAG)=∠2+∠DAG(三角形内角和定理),∠AGF=∠DAG+∠3(已知),
∴∠2=∠3(等式性质),
∴∠1=∠3(等量代换).
3. (2025·山东青岛崂山区期末)如图,∠ACE= ∠DCE,∠B= 35°,∠DCE= 50°,则∠A= (
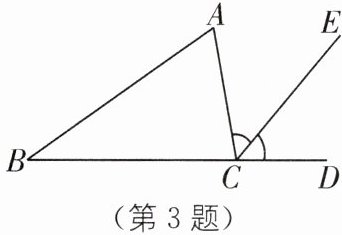
A.65°
B.75°
C.85°
D.95°
A
).
A.65°
B.75°
C.85°
D.95°
答案:
A [解析]
∵∠ACE=∠DCE,∠DCE=50°,
∴∠ACE=50°,
∴∠ACD=∠ACE+∠DCE=100°.
∵∠ACD=180°-∠ACB=180°-(180°-∠B-∠A)=∠B+∠A,∠B=35°,
∴∠A=∠ACD-∠B=100°-35°=65°. 故选 A.
∵∠ACE=∠DCE,∠DCE=50°,
∴∠ACE=50°,
∴∠ACD=∠ACE+∠DCE=100°.
∵∠ACD=180°-∠ACB=180°-(180°-∠B-∠A)=∠B+∠A,∠B=35°,
∴∠A=∠ACD-∠B=100°-35°=65°. 故选 A.
4. (2025·金华金东区期中)如图,在△ABC 中,∠BAC= 100°,AD⊥BC 于 D 点,AE 平分∠BAC 交 BC 于点 E. 若∠C= 25°,则∠DAE 的度数为
15°
.
答案:
15°
5. 中考新考法 在动态变化中寻找定值 (2024·河南开封顺河区求实中学月考)如图(1),在△ABC 中,BD 平分∠ABC,CD 平分∠ACB.
(1)若∠A= 80°,则∠BDC 的度数为______
(2)若∠A= α,直线 MN 经过点 D.
①如图(2),若 MN//AB,求∠NDC-∠MDB 的度数(用含α的代数式表示);
②如图(3),若 MN 绕点 D 旋转,分别交线段 BC,AC 于点 M,N,试问在旋转过程中∠NDC-∠MDB 的度数是否会发生改变?若不变,求出∠NDC-∠MDB 的度数(用含α的代数式表示);若改变,请说明理由.
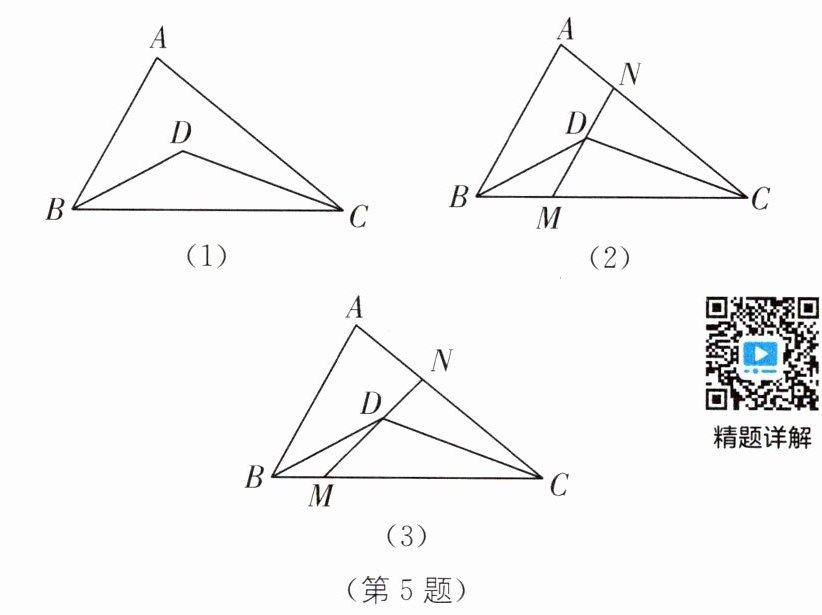
(1)若∠A= 80°,则∠BDC 的度数为______
130°
;(2)若∠A= α,直线 MN 经过点 D.
①如图(2),若 MN//AB,求∠NDC-∠MDB 的度数(用含α的代数式表示);
②如图(3),若 MN 绕点 D 旋转,分别交线段 BC,AC 于点 M,N,试问在旋转过程中∠NDC-∠MDB 的度数是否会发生改变?若不变,求出∠NDC-∠MDB 的度数(用含α的代数式表示);若改变,请说明理由.

(2)①$90^{\circ}-\frac{1}{2}\alpha$;②∠NDC-∠MDB 的度数不变,为$90^{\circ}-\frac{1}{2}\alpha$。
答案:
(1)130° [解析]
∵BD 平分∠ABC,CD 平分∠ACB,
∴∠DBC= $\frac{1}{2}$∠ABC,∠DCB= $\frac{1}{2}$∠ACB,
∴∠BDC=180°-(∠DBC+∠DCB)=180°- $\frac{1}{2}$(∠ABC+∠ACB)=180°- $\frac{1}{2}$(180°-∠A)=90°+ $\frac{1}{2}$∠A.
∵∠A=80°,
∴∠BDC=90°+ $\frac{1}{2}$×80°=130°.
(2)①
∵MN//AB,
∴∠A=∠DNC,∠ABD=∠MDB,
∴∠NDC-∠MDB=180°-∠A- $\frac{1}{2}$∠ACB- $\frac{1}{2}$∠ABC=180°-α- $\frac{1}{2}$(180°-α)=90°- $\frac{1}{2}$α.
②∠NDC-∠MDB 的度数不变. 理由如下:
∵∠NDC-∠MDB=180°-∠MDC-∠MDB=180°-(180°-∠DMC-∠DCM)-∠MDB=∠DMC+∠DCM-∠MDB=180°-∠DMB+∠DCM-∠MDB=180°-(180°-∠DBM-∠BDM)+∠DCM-∠MDB=∠DBM+∠BDM+∠DCM-∠MDB= $\frac{1}{2}$∠ABC+ $\frac{1}{2}$∠ACB= $\frac{1}{2}$(180°-α)=90°- $\frac{1}{2}$α,
∴∠NDC-∠MDB 的度数不变.
(1)130° [解析]
∵BD 平分∠ABC,CD 平分∠ACB,
∴∠DBC= $\frac{1}{2}$∠ABC,∠DCB= $\frac{1}{2}$∠ACB,
∴∠BDC=180°-(∠DBC+∠DCB)=180°- $\frac{1}{2}$(∠ABC+∠ACB)=180°- $\frac{1}{2}$(180°-∠A)=90°+ $\frac{1}{2}$∠A.
∵∠A=80°,
∴∠BDC=90°+ $\frac{1}{2}$×80°=130°.
(2)①
∵MN//AB,
∴∠A=∠DNC,∠ABD=∠MDB,
∴∠NDC-∠MDB=180°-∠A- $\frac{1}{2}$∠ACB- $\frac{1}{2}$∠ABC=180°-α- $\frac{1}{2}$(180°-α)=90°- $\frac{1}{2}$α.
②∠NDC-∠MDB 的度数不变. 理由如下:
∵∠NDC-∠MDB=180°-∠MDC-∠MDB=180°-(180°-∠DMC-∠DCM)-∠MDB=∠DMC+∠DCM-∠MDB=180°-∠DMB+∠DCM-∠MDB=180°-(180°-∠DBM-∠BDM)+∠DCM-∠MDB=∠DBM+∠BDM+∠DCM-∠MDB= $\frac{1}{2}$∠ABC+ $\frac{1}{2}$∠ACB= $\frac{1}{2}$(180°-α)=90°- $\frac{1}{2}$α,
∴∠NDC-∠MDB 的度数不变.
查看更多完整答案,请扫码查看


