第119页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
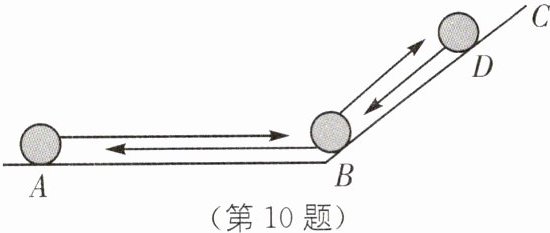
10. 新情境 轨道运动 小球沿着如图所示的轨道(由光滑的水平轨道AB和斜坡轨道BC组成)运动,从点A开始到点D再返回到点A.小球在AB上做匀速运动,下列表示小球运动的路程y随着时间x变化的图象中,合理的是(
(第10题)
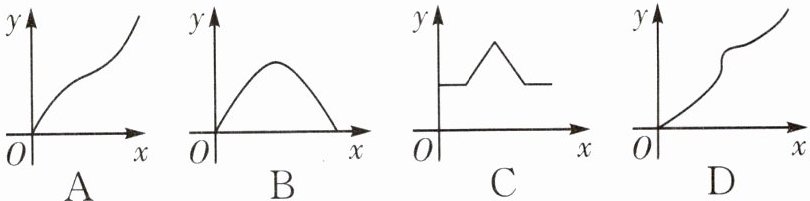
A
B
C D
A
).(第10题)


A
B
C D
答案:
A [解析]由题意可知,小球的路程由0开始,随时间x的增大而增大,故选项C不合题意;小球从A运动到B时,速度比较快,图象较陡;从B到D时,速度较慢,图象变缓;从D到A时,速度变快,图象变陡,故选项B,D不合题意,选项A符合题意.故选A.
11.(2025·江苏苏州期末)某学校科技社团成员组装了一艘舰艇模型,并在一条笔直河道内进行往返航行测试,中途设置一个观测点P.他们根据测试结果绘制了如图所示函数图象,其中t(min)表示航行时间,s(m)表示舰艇模型离出发点距离.已知水流速度为30 m/min.
(1)根据图象回答:在OA段,舰艇模型
(2)该舰艇模型先后两次经过观测点P时间差为1.6 min,求观测点P离出发点距离.
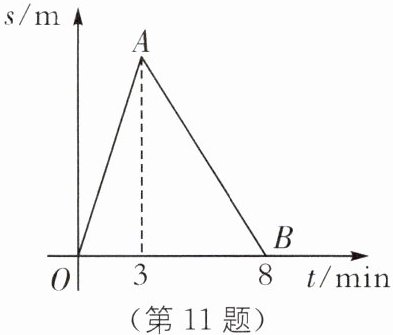
(第11题)精题详解
(1)根据图象回答:在OA段,舰艇模型
顺
水航行(填"顺"或"逆");该舰艇模型在静水中航行速度为120
m/min; (2)该舰艇模型先后两次经过观测点P时间差为1.6 min,求观测点P离出发点距离.

(第11题)精题详解
设点P距离出发点的距离为y m,由(1)可知舰艇模型在静水中的航行速度为120 m/min,水流速度为30 m/min,所以顺水速度为120+30=150(m/min),逆水速度为120-30=90(m/min)。去程用时3 min,起点与终点的距离为3×150=450(m),则点P距离终点的路程为(450-y)m。设从点P去程到终点用时t₁min,从终点返程到点P用时t₂min,根据题意得t₁+t₂=1.6。因为t₁=(450-y)/150,t₂=(450-y)/90,所以(450-y)/150+(450-y)/90=1.6,解得y=360。答:观测点P离出发点的距离为360米。
答案:
(1)顺 120 [解析]设顺水速度为$v_{顺}$,逆水速度为$v_{逆}$,$v_{顺}=v_{静}+v_{水}$,$v_{逆}=v_{静}-v_{水}$,
∴$v_{顺}>v_{逆}$.在无法快速直接得出结论时,可通过数形结合进行判断根据图象可知,从起点到终点,即OA段,用时3 min,从终点到起点,即AB段,用时8-3=5(min),路程相同,时间越短,速度越大,
∴在OA段,舰艇模型是顺水航行.设$v_{静}=x$m/min,$v_{水}=30$m/min,
∴3(x+30)=5(x-30),解得x=120,故该舰艇模型在静水中的航行速度为120 m/min.
(2)设点P距离出发点的距离为y m,由
(1)可知$v_{静}=120$m/min,$v_{水}=30$m/min,去程用时3 min,则起点与终点的距离为3×(120+30)=3×150=450(m),
∴点P距离终点的路程为(450-y)m.设从点P去程到终点用时$t_1$min,从终点返程到点P用时$t_2$min,
∴$t_1+t_2=1.6$.
∵$t_1=\frac{450-y}{120+30}=\frac{450-y}{150}$,$t_2=\frac{450-y}{120-30}=\frac{450-y}{90}$,
∴$\frac{450-y}{150}+\frac{450-y}{90}=1.6$,解得y=360,
∴观测点P离出发点的距离为360米.
(1)顺 120 [解析]设顺水速度为$v_{顺}$,逆水速度为$v_{逆}$,$v_{顺}=v_{静}+v_{水}$,$v_{逆}=v_{静}-v_{水}$,
∴$v_{顺}>v_{逆}$.在无法快速直接得出结论时,可通过数形结合进行判断根据图象可知,从起点到终点,即OA段,用时3 min,从终点到起点,即AB段,用时8-3=5(min),路程相同,时间越短,速度越大,
∴在OA段,舰艇模型是顺水航行.设$v_{静}=x$m/min,$v_{水}=30$m/min,
∴3(x+30)=5(x-30),解得x=120,故该舰艇模型在静水中的航行速度为120 m/min.
(2)设点P距离出发点的距离为y m,由
(1)可知$v_{静}=120$m/min,$v_{水}=30$m/min,去程用时3 min,则起点与终点的距离为3×(120+30)=3×150=450(m),
∴点P距离终点的路程为(450-y)m.设从点P去程到终点用时$t_1$min,从终点返程到点P用时$t_2$min,
∴$t_1+t_2=1.6$.
∵$t_1=\frac{450-y}{120+30}=\frac{450-y}{150}$,$t_2=\frac{450-y}{120-30}=\frac{450-y}{90}$,
∴$\frac{450-y}{150}+\frac{450-y}{90}=1.6$,解得y=360,
∴观测点P离出发点的距离为360米.
12.(2023·河北中考)如图一种轨道示意图,其中$\overset{\frown}{ADC}和\overset{\frown}{ABC}$均为半圆,点M,A,C,N依次在同一直线上,且$AM= CN$,现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同速度匀速移动,其路线分别为$M→A→D→C→N$ 和$N→C→B→A→M$.若移动时间为x,两个机器人之间距离为y,则y x关系图象大致(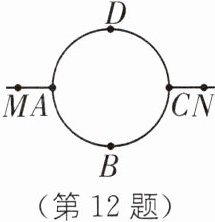
(第12题)
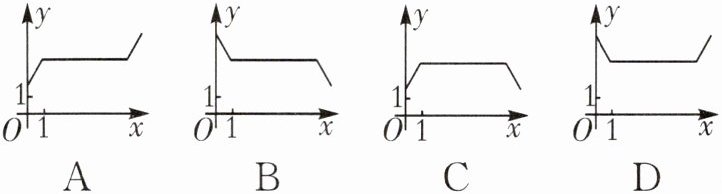
D
).
(第12题)

答案:
D [解析]设圆的半径为R,由题意,可得机器人(看成点)分别从M,N两点同时出发,
∴两个机器人最初的距离是AM+CN+2R.
∵两个机器人速度相同,
∴同时到达点A,C,
∴两个机器人之间的距离y越来越小,故排除A,C;当两个机器人分别沿A→D→C和C→B→A移动时,此时两个机器人之间的距离是2R,保持不变,当机器人分别沿C→N和A→M移动时,此时两个机器人之间的距离越来越大,故排除B.故选D.
∴两个机器人最初的距离是AM+CN+2R.
∵两个机器人速度相同,
∴同时到达点A,C,
∴两个机器人之间的距离y越来越小,故排除A,C;当两个机器人分别沿A→D→C和C→B→A移动时,此时两个机器人之间的距离是2R,保持不变,当机器人分别沿C→N和A→M移动时,此时两个机器人之间的距离越来越大,故排除B.故选D.
查看更多完整答案,请扫码查看


