《2025年实验班提优训练八年级数学上册浙教版》

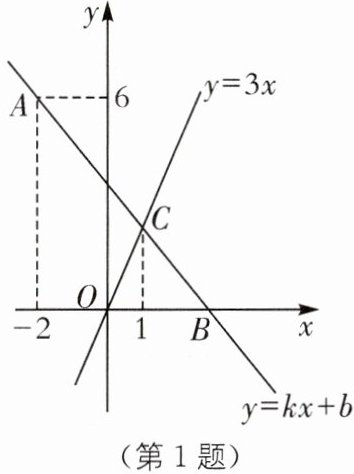
1. 如图,在平面直角坐标系中,一次函数 $ y= kx+b $ 的图象经过点 $ A(-2,6) $,且与 $ x $ 轴相交于点 $ B $,与正比例函数 $ y= 3x $ 的图象相交于点 $ C $,点 $ C $ 的横坐标为 1.
(1)求 $ k,b $ 的值;
(2)请直接写出方程组 $ \begin{cases} kx-y= -b, \\ 3x-y= 0 \end{cases} $ 的解;
(3)若点 $ D $ 在 $ y $ 轴上,且满足 $ S_{\triangle DOC}= S_{\triangle BOC} $,求点 $ D $ 的坐标.

答案： 1.
(1)当x=1时,y=3x=3,
∴点C坐标为(1,3).直线y=kx+b经过(-2,6)和(1,3),则6=-2k+b，3=k+b，解得k=-1，b=4.
(2)方程组{kx - y = -b，3x - y = 0}的解是{x = 1，y = 3}.
(3)由
(1)知,一次函数的表达式为y=-x+4.当y=0时,即0=-x+4,
∴x=4.设点D坐标为(0,a),
∴OD=|a|.
∵S△DOC = S△BOC，
∴$\frac{1}{2}$|a|×1 = $\frac{1}{2}$×4×3,解得a = ±12,
∴点D的坐标为(0,12)或(0,-12).

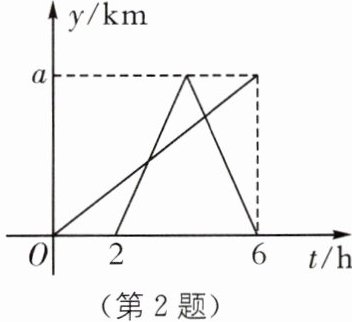
2. (2025·湖北武汉青山区期末)一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,往返速度的大小不变,两车离甲地的距离 $ y(\text{km}) $ 与慢车行驶时间 $ t(\text{h}) $ 之间的函数关系如图所示.则下列结论:
①快车比慢车晚出发 2 h;
②快车速度是慢车速度的 2 倍;
③慢车从出发到两车第一次相遇时,所走的路程为 $ \frac{a}{2}\ \text{km} $;
④若两车第二次相遇地距乙地距离为 90 km,则 $ a= 360\ \text{km} $.
其中正确的有______①③④.(请填写序号)

答案： 2.①③④ [解析]由图象可得,快车比慢车晚出发2h,故①正确；快车的速度为$\frac{2a}{6 - 2}$ = $\frac{a}{2}$(km/h),慢车的速度为$\frac{a}{6}$km/h,
∵$\frac{a}{2}$÷$\frac{a}{6}$ = 3,
∴快车速度是慢车速度的3倍,故②错误；设慢车行驶mh两车第一次相遇,则$\frac{1}{6}$am = $\frac{1}{2}$a(m - 2),解得m = 3,
∴慢车所走的路程为$\frac{1}{6}$a×3 = $\frac{a}{2}$(km),故③正确；设慢车行驶nh两车第二次相遇,则$\frac{1}{6}$an + $\frac{1}{2}$a(n - $\frac{6 - 2}{2}$ - 2) = a,解得n = $\frac{9}{2}$,此时慢车距乙地的距离为a - $\frac{1}{6}$a×$\frac{9}{2}$ = $\frac{1}{4}$a = 90,解得a = 360,故④正确.

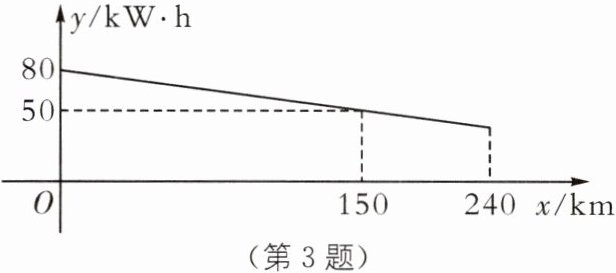
3. 新情境 发展新能源汽车 (2024·陕西中考)我国新能源汽车快速健康发展,续航里程不断提升,王师傅驾驶一辆纯电动汽车从 $ A $ 市前往 $ B $ 市,他驾车从 $ A $ 市一高速公路入口驶入时,该车的剩余电量是 80 kW·h,行驶了 240 km 后,从 $ B $ 市一高速公路出口驶出,已知该车在高速公路上行驶的过程中,剩余电量 $ y(\text{kW·h}) $ 与行驶路程 $ x(\text{km}) $ 之间的关系如图所示.
(1)求 $ y $ 与 $ x $ 之间的表达式.
(2)已知这辆车的“满电量”为 100 kW·h,求王师傅驾车从 $ B $ 市这一高速公路出口驶出时,该车的剩余电量占“满电量”的百分之多少?

答案： 3.
(1)设y与x之间的关系式为y=kx+b,将(0,80),(150,50)代入,得{80 = b，50 = 150k + b}，解得{b = 80，k = -0.2}，
∴y与x之间的关系式为y=-0.2x+80.
(2)当x=240时,y=-0.2×240+80=32,$\frac{32}{100}$×100% = 32%.故该车的剩余电量占“满电量”的32%.

4. (2024·宁波慈溪期末)公司派甲车把货物从 $ A $ 地运往 $ B $ 地,出发几分钟后,公司发现甲车忘带货物清单,于是派乙车去追赶甲车,乙车刚出发 2 分钟,甲车也发现清单忘在公司,立刻原路返回,几分钟后遇到乙车,乙车把清单交给甲车后,两车同时掉头返回,在行驶 6 分钟后甲车到达 $ B $ 地,乙车回到 $ A $ 地,已知甲、乙两车距 $ A $ 地的路程 $ y $ 与甲车出发的时间 $ x $ 之间的关系如图所示,整个过程中甲、乙两车速度不变,请结合图象回答下列问题:
(1)甲的速度为______米/分钟,乙的速度为______米/分钟;
(2)求 $ a $ 的值;
(3)求乙车在送清单途中距离甲车 5250 米时,$ x $ 的值.

答案：
4.
(1)500 750 [解析]甲车的行驶速度为$\frac{7500 - 4500}{6}$ = 500(米/分钟),乙车行驶速度为$\frac{4500}{6}$ = 750(米/分钟).
(2)如图所示.

由题意可知,乙车速度不变,故DN段和CN段所用时间均为6分钟,则甲车走MN段路程用时为6 - 2 = 4(分钟),
∴MN段路程为500×4 = 2000(米),
∴点M纵坐标为4500 + 2000 = 6500,
∴甲车在OM段所用时间为6500÷500 = 13(分钟),
∴a = 13 + 4 + 6 = 23.
(3)由
(2),可得D(11,0),N(17,4500),C(23,0).①设甲发现未带清单之前,乙车出发t分钟时与甲车相距5250米,根据题意,得500(11 + t) - 750t = 5250,解得t = 1,此时x = l1 + t = l2.②设乙车把清单交给甲车后,两车同时掉头返回,经过m分钟时相距5250米,根据题意,得(750 + 500)m = l5l5m = l5l50÷l250 = 4.2,此时x = l7 + m = l2l.l.综上,x的值为l2或l2.l.