《2025年实验班提优训练八年级数学上册浙教版》

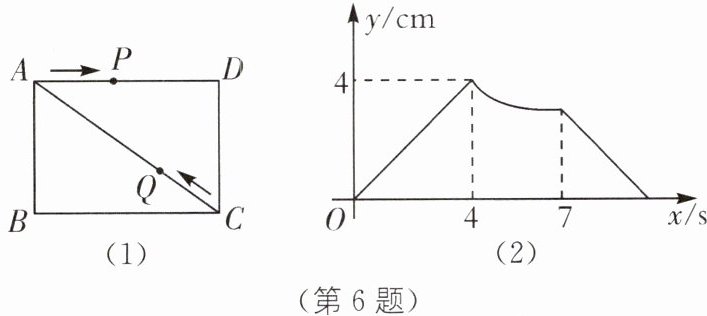
6. (河南自主招生)如图(1),在长方形 ABCD 中,动点 P 从点 A 出发沿 A→D→C 方向运动到点 C 停止,动点 Q 从点 C 出发沿 C→A 方向运动到点 A 停止,若点 P,Q 同时出发,点 P 的速度为 2 cm/s,点 Q 的速度为 1 cm/s,设运动时间为 x s,AP-CQ= y cm,y 与 x 的函数关系图象如图(2)所示,则 AC 的长为(C).

A.8 cm
B.9 cm
C.10 cm
D.14 cm

答案： C [解析]根据题意，结合函数图象，可知，当0≤x＜4时，点P在AD上运动；当x=4时，点P运动到点D，即AD=2×4=8(cm)；当4＜x＜7时，点P在DC上运动；当x=7时，点P运动到点C，即CD=2×7-8=6(cm). 在长方形ABCD中，AD=8cm，CD=6cm，则AC=10cm. 故选 C.

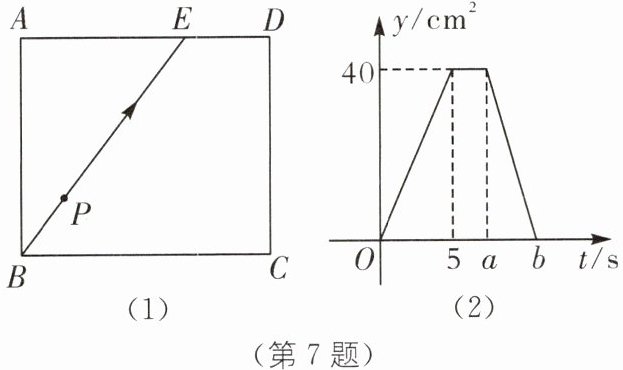
7. (2025·安徽安庆第四中学期末)如图(1),在长方形 ABCD 中,AB= 8 cm,E 是边 AD 上一点,且 AE= 6 cm,点 P 从点 B 出发,沿折线 BE→ED→DC 匀速运动,运动到点 C 停止.点 P 的运动速度为 2 cm/s,运动时间为 t(s),△BPC 的面积为$ y(cm^2),y $与 t 的函数关系图象如图(2)所示,则下列结论错误的是( C ).

A.BC= 10 cm
B.a= 7
C.b= 10.5
D.当 t= 8 s 时$,y= 30 cm^2$

答案： C [解析]
∵四边形ABCD为长方形，
∴AB=DC，BC=AD. A. 当t=5时，点P运动到点E，此时S△BPC=$\frac{1}{2}$BC·AB=$\frac{1}{2}$×8×BC=40，解得BC=10，则A正确，故本选项不符合题意；B. 由AD=BC=10，AE=6，得ED=AD-AE=4，结合点P的运动速度为2cm/s，得tED=$\frac{ED}{2}$=2s，那么a=5+2=7，则B正确，故本选项不符合题意；C. 由DC=AB=8，点P的运动速度为2cm/s，得tDC=$\frac{DC}{2}$=4，则b=7+4=11，C错误，故本选项符合题意；D. 当t=8s时，y=$\frac{1}{2}$BC·[DC-(8-7)×2]=$\frac{1}{2}$×10×6=30(cm²)，则D正确，故本选项不符合题意. 故选 C.

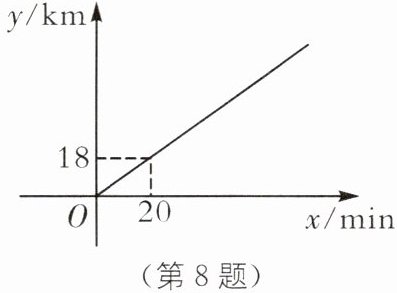
8. 甲车从 A 地出发匀速行驶,它行驶的路程 y(单位:km)与行驶的时间 x(单位:min)之间的函数关系如图所示.甲车出发 20 min 后,乙车从 A 地出发沿同一路线匀速行驶.若乙车经过 20 min~30 min 追上甲车,则乙车的速度 v(单位:km/min)的取值范围是______$\frac{3}{2}$≤v≤$\frac{9}{5}$.

答案： $\frac{3}{2}$≤v≤$\frac{9}{5}$ [解析]根据图象，得甲车的速度为18÷20=$\frac{9}{10}$(km/min)，设甲车出发t min后乙车追上甲车. 根据题意，得40≤t≤50，则$\frac{9}{10}$t=v(t-20)，整理，得v=$\frac{0.9t}{t-20}$=$\frac{9t}{10(t-20)}$=$\frac{9}{10-\frac{200}{t}}$，
∴v随t的增大而减小. 当t=50时，v取最小值，v=$\frac{3}{2}$；当t=40时，v取最大值，v=$\frac{9}{5}$，
∴$\frac{3}{2}$≤v≤$\frac{9}{5}$.

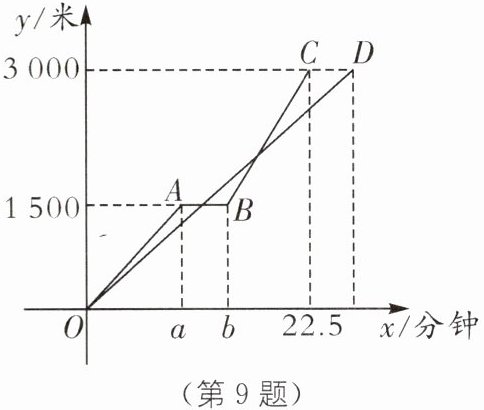
9. (2025·安徽池州期中改编)小张和妈妈同时从家沿同一直道骑自行车去公园.妈妈先以 150 米/分钟的速度骑行一段时间后,休息了 5 分钟,再以 m 米/分钟的速度到达公园,小张始终以同一速度骑行,两人离家的距离 y(米)与时间 x(分钟)的关系如图所示,请结合图象,回答:
a=10分,b=15分,m=200米/分.

答案： 10 15 200

10. 小明家有一大一小两个圆柱形的杯子,大杯子的杯口半径刚好是小杯子杯口半径的 2 倍,他将小杯子杯口朝上放入大杯子中,组成如图(1)所示的一个容器,并匀速向小杯子中注水,当小杯子注满后,水溢到大杯子中,直至整个容器注满水,注水过程中容器内水位最大高度 h(cm)与时间 t(s)之间的关系如图(2)所示(小杯子的厚度忽略不计).
根据图中提供的信息,回答下列问题:
(1)小杯子的高度为6cm,将小杯子注满水所用的时间为5s,大杯子的高是小杯子高的2倍;
(2)请求出图象中 a 的值,并说明它表示的实际意义;
设小杯子的杯口半径为r cm，则大杯子的杯口半径为2r cm，将小杯子注满需要的水量为6πr²cm³，当大杯子中水位高度是6cm时，需要的水量为π·(2r)²×6-6πr²=18πr²(cm³).
∵当大杯子中水位高度是6cm时，所用的时间为5×$\frac{18πr²}{6πr²}$=15(s)，15+5=20(s)，
∴a的值为20，它表示20s时，大杯子中水位高度是6cm，与小杯子高度齐平.
(3)求整个容器注满水所需要的时间.
$\frac{12πr²·(2r)²}{6πr²}$×5=40(s). 故整个容器注满水所需要的时间为40s.

答案：
(1)6 5 2
(2)设小杯子的杯口半径为r cm，则大杯子的杯口半径为2r cm，将小杯子注满需要的水量为6πr²cm³，当大杯子中水位高度是6cm时，需要的水量为π·(2r)²×6-6πr²=18πr²(cm³).
∵当大杯子中水位高度是6cm时，所用的时间为5×$\frac{18πr²}{6πr²}$=15(s)，15+5=20(s)，
∴a的值为20，它表示20s时，大杯子中水位高度是6cm，与小杯子高度齐平.
(3)$\frac{12πr²·(2r)²}{6πr²}$×5=40(s). 故整个容器注满水所需要的时间为40s.
易错警示 解答本题需要注意：题意中提到小杯子的口是朝上的，所以当水位上升到小杯子口时，水才进入大杯子中，直到大杯子中水与小杯中水平齐为止，水位是不变的.