《2025年实验班提优训练八年级数学上册浙教版》

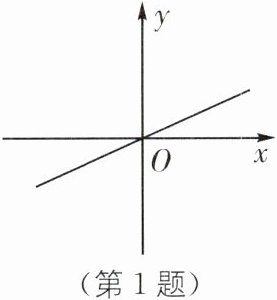
1. (2024·德阳中考)正比例函数$y= kx(k≠0)$的图象如图所示,则k的值可能是(A).

A.$\frac {1}{2}$
B.$-\frac {1}{2}$
C.-1
D.$-\frac {1}{3}$

答案： 1.A [解析]
∵正比例函数图象经过第一、三象限，
∴k＞0，
∴选项 A 符合题意.故选 A.

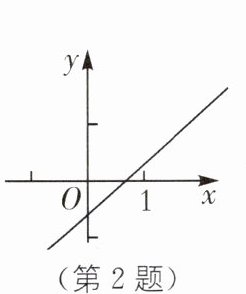
2. (教材P174例1·变式)(2024·杭州上城区一模)在平面直角坐标系中,一次函数$y= x+a(a≠0)$的图象如图所示,若$y= ax+1$的图象与x轴交于$(m,0)$,则下列判断正确的是(D).

A.$m＜-1$
B.$-1＜m＜0$
C.$0＜m＜1$
D.$m＞1$

答案： 2.D [解析]由函数图象可知，-1＜a＜0.
∵y=ax+1的图象与x轴交于(m,0)，
∴当 y=0 时，ax+1=0.
∴$x=-\frac{1}{a}.$
∴$m=-\frac{1}{a}，$令 a=-0.5，则 -a=0.5.
∴$-\frac{1}{a}=\frac{1}{0.5}=2＞1，$
∴m＞1.故选 D.

3. (2024·自贡中考)一次函数$y= (3m+1)x-2$的值随x的增大而增大,请写出一个满足条件的m的值1.

答案： 3.1(答案不唯一)[解析]
∵y=(3m+1)x-2 的值随 x 的增大而增大，
∴3m+1＞0.
∴$m＞-\frac{1}{3}.$
∴m 的值可以为 1.(答案不唯一，满足$ m＞-\frac{1}{3}$即可)

4. (2024·甘肃中考)已知一次函数$y= -2x+4$,当自变量$x＞2$时,函数y的值可以是-2(写出一个合理的值即可).

答案： 4.-2(答案不唯一)[解析]根据 x＞2，选择 x=3，此时 y=-2×3+4=-2.

5. (安徽蚌埠二中自主招生)已知一次函数$y= (2k-1)x+k+2的图象在-1≤x≤2$内的一段都在x轴上方,求k的取值范围.

答案： 5.①当 2k-1＞0，即$ k＞\frac{1}{2}$时，y 随 x 的增大而增大，只需(2k-1)·(-1)+k+2＞0，解得 k＜3.故$ \frac{1}{2}＜k＜3；$②当 2k-1＜0，即$ k＜\frac{1}{2}$时，y 随 x 的增大而减小，只需(2k-1)×2+k+2＞0，解得 k＞0.故$ 0＜k＜\frac{1}{2}.$综上所述，0＜k＜3，且$ k≠\frac{1}{2}.$

6. (2025·广东深圳期末)如图,一次函数$y_{1}= -x+a与y_{2}= bx-4的图象交于点P(1,-3)$,下列结论正确的是(C).
A.方程$-x+a= bx-4的解是x= -3$
B.不等式$-x+a＞-3和不等式bx-4＞-3$的解集相同
C.不等式组$bx-4＜-x+a＜0的解集是-2＜x＜1$
D.方程组$\left\{\begin{array}{l} y= -x+a,\\ y= bx-4\end{array} \right. 的解为\left\{\begin{array}{l} x= a,\\ y= -3\end{array} \right. $

答案： 6.C [解析]A.由图象可得直线 y₁=-x+a 与 y₂=bx-4(b≠0)的图象交于点 P(1,-3).
∴方程 -x+a=bx-4 的解是 x=1，故 A 不符合题意；B.由图象可知，不等式 -x+a＞-3 的解集是 x＜1，不等式 bx-4＞-3 的解集是 x＞1，故 B 不符合题意；C.将 P(1,-3)代入 y₁=-x+a，得 -3=-1+a，解得 a=-2，
∴y₁=-x-2，将 y=0 代入 y₁=-x-2，得 0=-x-2，解得 x=-2，
∴当 -2＜x＜1 时，直线 y₁=-x+a 在 x 轴下方且在直线 y₂=bx-4(b≠0)上方，
∴bx-4＜-x+a＜0 的解集是 -2＜x＜1，故 C 符合题意；D.方程组{y=-x+a,y=bx-4}的解为{x=1,y=-3}，故 D 不符合题意.故选 C.

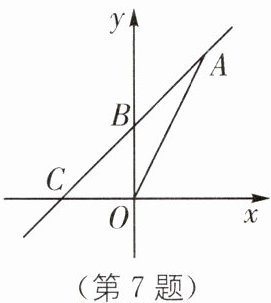
7. (2024·凉山州中考)如图,一次函数$y= kx+b的图象经过A(3,6),B(0,3)$两点,交x轴于点C,则$\triangle AOC$的面积为______.

9

答案： 7.9 [解析]将 A(3,6)，B(0,3)代入 y=kx+b，得{3k+b=6,b=3}，解得{k=1,b=3}，
∴直线 AB 的表达式为 y=x+3.当 y=0 时，x+3=0，解得 x=-3，
∴点 C 的坐标为(-3,0)，OC=3，
∴$S△AOC=\frac{1}{2}OC·$|yₐ|$=\frac{1}{2}×3×6=9.$

8. (2025·杭州余杭区期末)已知一次函数$y= (2m-1)x+m+2$.
(1)若该函数图象经过原点,求m的值;
(2)在该函数中,y随x的增大而增大,求m的取值范围;
(3)若$m= -1$,当$1≤y≤4$时,直接写出x的取值范围.

答案： 8.
(1)
∵该一次函数的图象经过原点(0,0)，
∴0=0+m+2，
∴m=-2.
(2)
∵该一次函数的函数值 y 随 x 的增大而增大，
∴2m-1＞0，
∴$m＞\frac{1}{2}. (3)$当 m=-1 时，此时 y=-3x+1.当 1≤y≤4 时，
∴{-3x+1≥1,-3x+1≤4}，解得 -1≤x≤0.故此时 x 的取值范围为 -1≤x≤0.