第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
18. 分类讨论思想 阅读以下材料:
已知两个正整数的和与积相等,求这两个正整数.
解:不妨设这两个正整数为a和b,且a≤b.
由题意,得ab= a+b,(*)
则ab= a+b≤b+b= 2b,所以a≤2.
因为a为正整数,所以a= 1或2.
①当a= 1时·,代入等式(*),得1·b= 1+b,b不存在;
②当a= 2时,代入等式(*),得2·b= 2+b,b= 2,
所以这两个正整数为2和2.
根据阅读材料的启示,思考是否存在三个正整数,它们的和与积相等.试说明你的理由.
]
已知两个正整数的和与积相等,求这两个正整数.
解:不妨设这两个正整数为a和b,且a≤b.
由题意,得ab= a+b,(*)
则ab= a+b≤b+b= 2b,所以a≤2.
因为a为正整数,所以a= 1或2.
①当a= 1时·,代入等式(*),得1·b= 1+b,b不存在;
②当a= 2时,代入等式(*),得2·b= 2+b,b= 2,
所以这两个正整数为2和2.
根据阅读材料的启示,思考是否存在三个正整数,它们的和与积相等.试说明你的理由.
]
答案:
存在.理由如下:假设存在三个正整数,它们的和与积相等.不妨设这三个正整数为a,b,c,且a≤b≤c,则abc=a+b+c,(* )所以abc=a+b+c≤c+c+c=3c,所以ab≤3.若a≥2,则b≥a≥2,所以ab≥4,与ab≤3矛盾.因此a=1,b=1或2或3.
利用不等式确定其中一个数的取值,再分类讨论
①当a=1,b=1时,代入等式(* ),得1+1+c=1×1·c,c不存在;
②当a=1,b=2时,代入等式(* ) ,得1+2+c=1×2·c,c=3;③当a=1,b=3时,代入等式(* ) ,得1+3+c=1×3·c,c=2,与b≤c矛盾,舍去.故a=1,b=2,c=3,因此假设成立,即存在三个正整数1,2,3,它们 的和与积相等.
利用不等式确定其中一个数的取值,再分类讨论
①当a=1,b=1时,代入等式(* ),得1+1+c=1×1·c,c不存在;
②当a=1,b=2时,代入等式(* ) ,得1+2+c=1×2·c,c=3;③当a=1,b=3时,代入等式(* ) ,得1+3+c=1×3·c,c=2,与b≤c矛盾,舍去.故a=1,b=2,c=3,因此假设成立,即存在三个正整数1,2,3,它们 的和与积相等.
19. 整体思想 中考新考法 解题方法型阅读理解题 [提出问题]已知x-y= 2,且x>1,y<0,试确定x+y的取值范围.
[分析问题]先根据已知条件用一个量(如y)去表示另一个量(如x),然后根据题中已知量x的取值范围,构建另一个量y的不等式,从而确定该量y的取值范围,同理再确定另一未知量x的取值范围,最后利用不等式的性质即可获解.
[解决问题]解:∵x-y= 2,∴x= y+2.
又x>1,∴y+2>1,∴y>-1.
又y<0,∴-1<y<0.①
同理,得1<x<2.②
由①+②,得-1+1<y+x<0+2,
∴x+y的取值范围是0<x+y<2.
[尝试应用]已知x-y=-3,且x<-1,y>1,求x+y的取值范围
[分析问题]先根据已知条件用一个量(如y)去表示另一个量(如x),然后根据题中已知量x的取值范围,构建另一个量y的不等式,从而确定该量y的取值范围,同理再确定另一未知量x的取值范围,最后利用不等式的性质即可获解.
[解决问题]解:∵x-y= 2,∴x= y+2.
又x>1,∴y+2>1,∴y>-1.
又y<0,∴-1<y<0.①
同理,得1<x<2.②
由①+②,得-1+1<y+x<0+2,
∴x+y的取值范围是0<x+y<2.
[尝试应用]已知x-y=-3,且x<-1,y>1,求x+y的取值范围
答案:
∵x-y=-3,
∴x=y-3.又x<-1,
∴y-3<一1,
∴y<2.又y>1,
∴1<y<2.①同理,得-2<x<一1,②由①十②,得1-2<y+x<2-1,
∴x+y的取值范围是-1<x+y<1.
∵x-y=-3,
∴x=y-3.又x<-1,
∴y-3<一1,
∴y<2.又y>1,
∴1<y<2.①同理,得-2<x<一1,②由①十②,得1-2<y+x<2-1,
∴x+y的取值范围是-1<x+y<1.
20. (2024·长春中考)不等关系在生活中广泛存在.如图,a,b分别表示两位同学的身高,c表示台阶的高度.图中两人的对话体现的数学原理是(
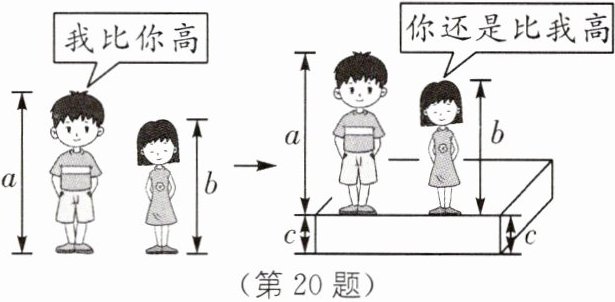
A.若a>b,则a+c>b+c
B.若a>b,b>c,则a>c
C.若a>b,c>0,则ac>bc
D.若a>b,c>0,则$\frac{a}{c}$>$\frac{b}{c}$
A
).
A.若a>b,则a+c>b+c
B.若a>b,b>c,则a>c
C.若a>b,c>0,则ac>bc
D.若a>b,c>0,则$\frac{a}{c}$>$\frac{b}{c}$
答案:
A [解析]由题意,得a>b,
∴a+c>b+c,
∴题图中两人的对话体现 的数学原理是若a>b,则a+c>b+c.故选A.
∴a+c>b+c,
∴题图中两人的对话体现 的数学原理是若a>b,则a+c>b+c.故选A.
查看更多完整答案,请扫码查看


