第112页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 如图,在平面直角坐标系中,A,B,C,D 四点的坐标分别是A(1,3),B(1,1),C(3,1),D(3,3),动点 P 从点 A 出发,在正方形边上按照A→B→C→D→A→…的方向不断移动,已知点 P 的移动速度为每秒1个单位长度,则第 2025 秒,点 P 的坐标是(
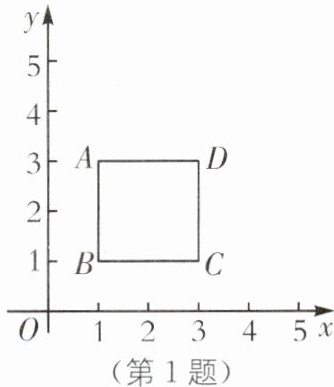
A.(1,2)
B.(3,1)
C.(3,2)
D.(1,3)
A
).
A.(1,2)
B.(3,1)
C.(3,2)
D.(1,3)
答案:
A [解析]
∵A(1,3),B(1,1),C(3,1),D(3,3),
∴AB=BC=CD=DA=2,
∴AB+BC+CD+DA=2×4=8.
∵点 P 的移动速度为每秒 1 个单位长度,
∴点 P 沿 A→B→C→D→A 移动一周所用的时间为 8÷1=8(秒).
∵2025÷8=253……1.
∴第 2024 秒,点 P 移动到点 A 的位置,
∴第 2025 秒点 P 的坐标是(1,2).故选 A.方法诠释 由题意得正方形 ABCD 的边长为 2,周长为 8.因为 2025÷8=253……1,可以推出点 P 在第 2024 秒时,移动到点 A 处,由此即可解决问题.
∵A(1,3),B(1,1),C(3,1),D(3,3),
∴AB=BC=CD=DA=2,
∴AB+BC+CD+DA=2×4=8.
∵点 P 的移动速度为每秒 1 个单位长度,
∴点 P 沿 A→B→C→D→A 移动一周所用的时间为 8÷1=8(秒).
∵2025÷8=253……1.
∴第 2024 秒,点 P 移动到点 A 的位置,
∴第 2025 秒点 P 的坐标是(1,2).故选 A.方法诠释 由题意得正方形 ABCD 的边长为 2,周长为 8.因为 2025÷8=253……1,可以推出点 P 在第 2024 秒时,移动到点 A 处,由此即可解决问题.
2. (2025·安徽蚌埠期中)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中箭头方向排列,如(0,0),(1,0),(1,1),(2,2),(2,1),(2,0),(3,0),…,根据规律探索可得,第 2024 个点的坐标为(
A.(63,7)
B.(63,15)
C.(64,7)
D.(64,15)
A
).A.(63,7)
B.(63,15)
C.(64,7)
D.(64,15)
答案:
A [解析]由图知,第一列有 1 个点,点的横坐标为 0,第二列有 2 个点,点的横坐标为 1,第三列有 3 个点,点的横坐标为 2,…,依次类推,第 n 列有 n 个点,点的横坐标为 n-1,且奇数列由上到下进行运动,偶数列点从下到上进行运动,
∴前几列点的总数为$\frac{n(n+1)}{2}$,
∴$\frac{n(n+1)}{2}$≤2024.
∵$\frac{63×64}{2}$=2016,
∴n=63,即第 2024 个点在第 64 列,
∴第 2024 个点的横坐标为 63.
∵2024-2016=8,64 为偶数列,
∴第 2024 个点的纵坐标为 7,
∴第 2024 个点坐标为(63,7).故选 A.
∴前几列点的总数为$\frac{n(n+1)}{2}$,
∴$\frac{n(n+1)}{2}$≤2024.
∵$\frac{63×64}{2}$=2016,
∴n=63,即第 2024 个点在第 64 列,
∴第 2024 个点的横坐标为 63.
∵2024-2016=8,64 为偶数列,
∴第 2024 个点的纵坐标为 7,
∴第 2024 个点坐标为(63,7).故选 A.
3. 中考新考法 新定义问题 在平面直角坐标系 xOy 中,对于点P(x,y),我们把点P'(-y+1,x+1)叫作点 P 的伴随点.已知点$A_1$的伴随点为$A_2,$点$A_2$的伴随点为$A_3,$点$A_3$的伴随点为$A_4,…,$这样依次得到点$A_1,A_2,A_3,…,Aₙ,…$若点$A_1$的坐标为(3,1),则点$A_2₀_2_5$的坐标为______
(3,1)
.
答案:
(3,1) [解析]
∵A₁的坐标为(3,1),
∴A₂(0,4),A₃(-3,1),A₄(0,-2),A₅(3,1),…,依此类推,每 4 个点为一个循环组依次循环.
∵2025÷4=506……1,
∴点 A₂₀₂₅的坐标与点 A₁的坐标相同,即为(3,1).思路引导 本题是对点的变化规律的考查,读懂题目信息.根据“伴随点”的定义依次求出各点,不难发现,每4 个点为一个循环组依次循环,用 2025 除以 4,根据余数的情况确定点 A₂₀₂₅的坐标即可.
∵A₁的坐标为(3,1),
∴A₂(0,4),A₃(-3,1),A₄(0,-2),A₅(3,1),…,依此类推,每 4 个点为一个循环组依次循环.
∵2025÷4=506……1,
∴点 A₂₀₂₅的坐标与点 A₁的坐标相同,即为(3,1).思路引导 本题是对点的变化规律的考查,读懂题目信息.根据“伴随点”的定义依次求出各点,不难发现,每4 个点为一个循环组依次循环,用 2025 除以 4,根据余数的情况确定点 A₂₀₂₅的坐标即可.
4. (2024·宁波江北区青藤书院月考)如图,动点 P 在平面直角坐标系中按图示方向运动,第一次从原点 O 运动到点$P_1(1,1),$第二次运动到点$P_2(2,1),$第三次运动到点$P_3(3,0),$第四次运动到点$P_4(4,-2),$第五次运动到点$P_5(5,0),$第六次运动到点$P_6(6,2),$按这样的运动规律,点$P_2₀_2_3$的纵坐标是(
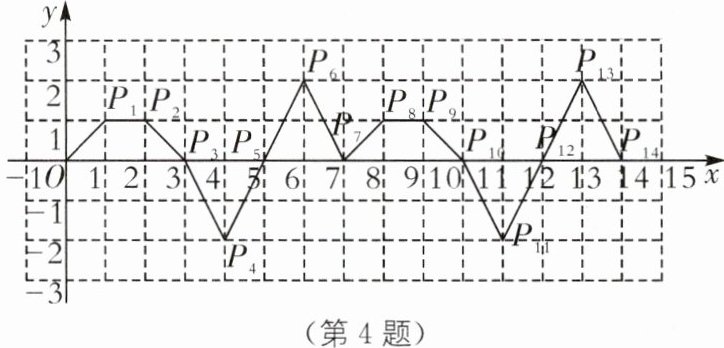
A.-2
B.0
C.1
D.2
B
).
A.-2
B.0
C.1
D.2
答案:
B [解析]观察图象,动点 P 第一次从原点 O 运动到点 P₁(1,1),第二次运动到点 P₂(2,1),第三次运动到点 P₃(3,0),第四次运动到点 P₄(4,-2),第五次运动到点 P₅(5,0),第六次运动到点 P₆(6,2),运动后的点的坐标特点可以发现规律,横坐标与次数相等,纵坐标每 7 次运动组成一个循环,P₁(1,1),P₂(2,1),P₃(3,0),P₄(4,-2),P₅(5,0),P₆(6,2),P₇(7,0),P₈(8,1),…,
∵2023=7×289,
∴动点 P₂₀₂₃的坐标是(2023,0),
∴动点 P₂₀₂₃的纵坐标是 0.故选 B.
∵2023=7×289,
∴动点 P₂₀₂₃的坐标是(2023,0),
∴动点 P₂₀₂₃的纵坐标是 0.故选 B.
5. (2024·宁波海曙区储能学校期中)如图,在平面直角坐标系中,第一次将△OAB 变换成$△OA_1B_1,$第二次将$△OA_1B_1$变换成$△OA_2B_2,$第三次将$△OA_2B_2$变换成$△OA_3B_3.$已知$A(1,4),A_1(2,4),A_2(4,4),A_3(8,4),B(2,0),B_1(4,0),B_2(8,0),B_3(16,0),…,$观察每次变换中△OAₙBₙ的顶点坐标有何变化,找出规律,推测点Aₙ的坐标是______,点Bₙ的坐标是______.
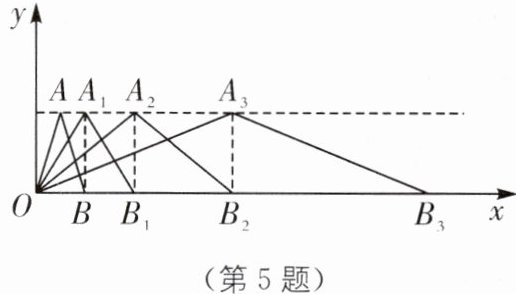

答案:
(2ⁿ,4) (2ⁿ⁺¹,0)
6. 将自然数按以下规律排列:
| | 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | … |
| 第一行 | 1 | 4 | 5 | 16 | 17 | … |
| 第二行 | 2 | 3 | 6 | 15 | 18 | … |
| 第三行 | 9 | 8 | 7 | 14 | 19 | … |
| 第四行 | 10 | 11 | 12 | 13 | 20 | … |
| 第五行 | 25 | 24 | 23 | 22 | 21 | … |
…………………| | | | | | | |
表中数2在第二行第一列,与有序数对(2,1)对应;数5与(1,3)对应;数14与(3,4)对应.根据这一规律,数2025对应的有序数对为__
| | 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | … |
| 第一行 | 1 | 4 | 5 | 16 | 17 | … |
| 第二行 | 2 | 3 | 6 | 15 | 18 | … |
| 第三行 | 9 | 8 | 7 | 14 | 19 | … |
| 第四行 | 10 | 11 | 12 | 13 | 20 | … |
| 第五行 | 25 | 24 | 23 | 22 | 21 | … |
…………………| | | | | | | |
表中数2在第二行第一列,与有序数对(2,1)对应;数5与(1,3)对应;数14与(3,4)对应.根据这一规律,数2025对应的有序数对为__
(45,1)
__.
答案:
(45,1)
查看更多完整答案,请扫码查看


