第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
13. 如图,每个小正方形的边长均为1,求证:△ABC是直角三角形.
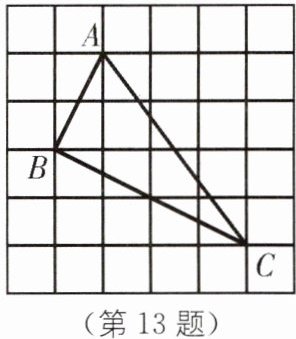

答案:
∵AC²=3²+4²=25,AB²=1²+2²=5,BC²=2²+4²=20,
∴AC²=AB²+BC²,
∴△ABC是直角三角形.
∵AC²=3²+4²=25,AB²=1²+2²=5,BC²=2²+4²=20,
∴AC²=AB²+BC²,
∴△ABC是直角三角形.
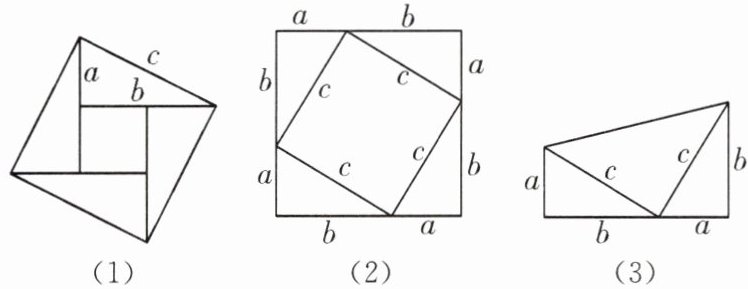
14. 勾股树模型 勾股定理是人类最伟大的科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图(1)),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理.(以下图形均满足证明勾股定理所需的条件)
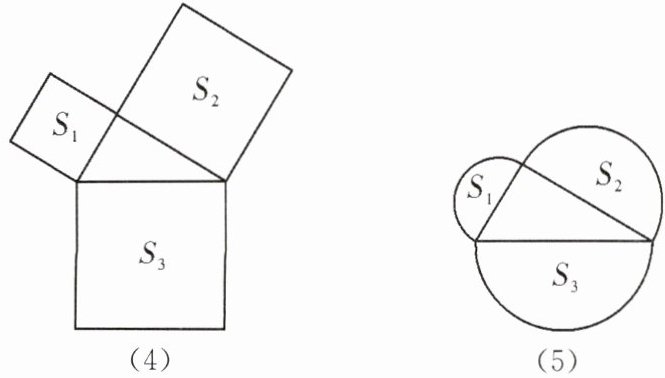
(2)①如图(4)(5)(6),以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足$S_1+S_2= S_3$的有
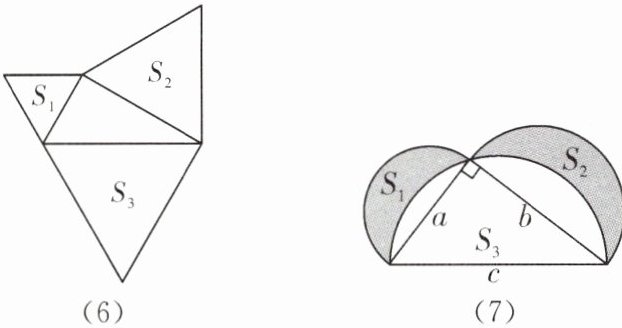
②如图(7)所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为$S_1,S_2,$直角三角形面积为$S_3,$请判断$S_1,S_2,S_3$的关系并证明.
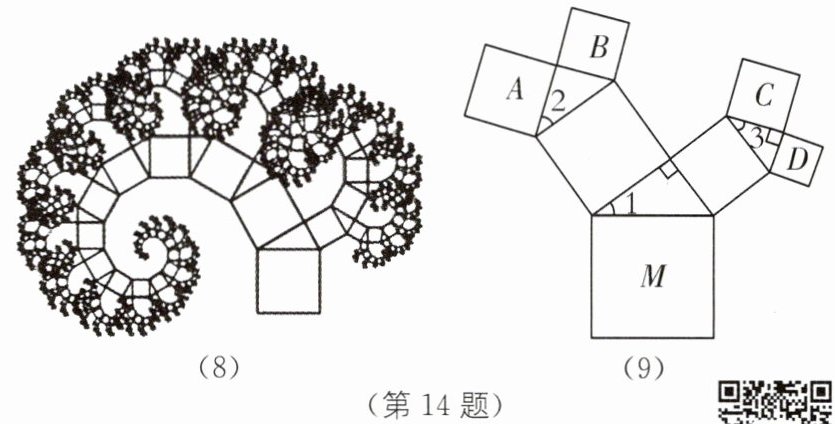
(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的士两直角边分别向外作正方形,重复这一过程就可以得到如图(8)所示的“勾股树”.在如图(9)所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,则$a^2+b^2+c^2+d^2=$
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理.(以下图形均满足证明勾股定理所需的条件)

(2)①如图(4)(5)(6),以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足$S_1+S_2= S_3$的有
3
个;
②如图(7)所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为$S_1,S_2,$直角三角形面积为$S_3,$请判断$S_1,S_2,S_3$的关系并证明.

(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的士两直角边分别向外作正方形,重复这一过程就可以得到如图(8)所示的“勾股树”.在如图(9)所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,则$a^2+b^2+c^2+d^2=$
$m^2$
.(结果可用含m的式子表示)
答案:
(1)①如果a,b为直角三角形的两条直角边的长,c为斜边的长,那么a²+b²=c².(直角三角形两条直角边的平方和等于斜边的平方.)②在题图
(1)中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,即c²=1/2ab×4+(b - a)²,化简,得a²+b²=c².在题图
(2)中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,即(a + b)²=c²+1/2ab×4,化简,得a²+b²=c².在题图
(3)中,梯形的面积等于三个直角三角形的面积的和,即1/2(a + b)(a + b)=1/2ab×2+1/2c²,化简,得a²+b²=c².
(2)①3 ②S₁+S₂=S₃.证明如下:
∵S₁+S₂=1/2π(a/2)²+1/2π(b/2)²=1/8π(a² + b²),S₃=1/2π(c/2)²=1/8πc²,且a² + b²=c²,
∴S₁+S₂=S₃.
(3)m²
(1)①如果a,b为直角三角形的两条直角边的长,c为斜边的长,那么a²+b²=c².(直角三角形两条直角边的平方和等于斜边的平方.)②在题图
(1)中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,即c²=1/2ab×4+(b - a)²,化简,得a²+b²=c².在题图
(2)中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,即(a + b)²=c²+1/2ab×4,化简,得a²+b²=c².在题图
(3)中,梯形的面积等于三个直角三角形的面积的和,即1/2(a + b)(a + b)=1/2ab×2+1/2c²,化简,得a²+b²=c².
(2)①3 ②S₁+S₂=S₃.证明如下:
∵S₁+S₂=1/2π(a/2)²+1/2π(b/2)²=1/8π(a² + b²),S₃=1/2π(c/2)²=1/8πc²,且a² + b²=c²,
∴S₁+S₂=S₃.
(3)m²
查看更多完整答案,请扫码查看


