《2025年实验班提优训练八年级数学上册浙教版》

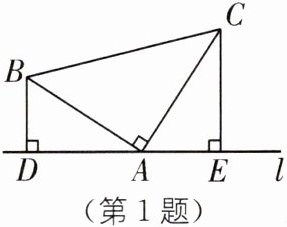
1. 某学习小组在探究三角形全等时,发现了下面这种典型的基本图形. 如图,已知：在△ABC中,∠BAC= 90°,AB= AC,直线 l 经过点 A,BD⊥直线 l,CE⊥直线 l,垂足分别为 D,E.求证：DE= BD+CE.

答案：
∵BD⊥直线l，CE⊥直线l，
∴∠BDA = ∠AEC = 90°。
∵∠BAC = 90°，
∴∠BAD + ∠CAE = 90°。
∵∠BAD + ∠ABD = 90°，
∴∠CAE = ∠ABD。
在△ADB和△CEA中，{∠ABD = ∠CAE，∠BDA = ∠AEC，AB = CA}
∴△ADB≌△CEA(AAS)，
∴AE = BD，AD = CE，
∴DE = AE + AD = BD + CE。
思路引导：本题主要考查全等三角形的判定和性质，由一线三等角的模型证明△ADB和△CEA全等得到BD = AE，CE = AD即可得证。

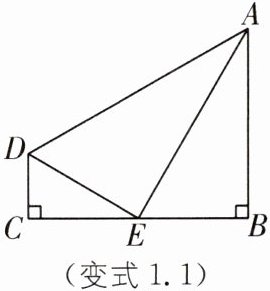
变式 1.1 实验班原创 如图,∠B= 90°,∠C= 90°,E为 BC 的中点,AE⊥DE,DE 平分∠ADC. 求证：(1)AE 是∠DAB 的平分线；(2)AD= DC+AB.

答案：

(1)如图，过点E作EF⊥AD于点F。

易知∠DFE = 90°，则∠DFE = ∠C。
∵DE平分∠ADC，
∴∠FDE = ∠CDE。
在△DCE和△DFE中，{∠C = ∠DFE，∠CDE = ∠FDE，DE = DE}
∴△DCE≌△DFE(AAS)，
∴CE = FE，DC = DF，∠CED = ∠FED。
∵AE⊥DE，
∴∠AED = 90°，
∴∠CED + ∠AEB = 90°，∠DEF + ∠AEF = 90°。
又∠CED = ∠FED，
∴∠AEF = ∠AEB。
∵E是BC的中点，
∴CE = BE，
∴FE = BE。
在△ABE和△AFE中，{BE = FE，∠AEB = ∠AEF，AE = AE}
∴△ABE≌△AFE(SAS)，
∴∠EAB = ∠EAF，即AE是∠DAB的平分线。
(2)由
(1)，得DC = DF，AB = AF，
∴AD = DF + AF = DC + AB。
归纳总结：本题主要考查了全等三角形的判定和性质、角平分线的定义等知识，灵活运用这些知识解决问题是解题的关键。

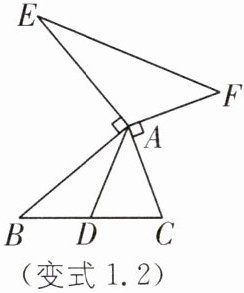
变式 1.2 如图,AD 是△ABC 的中线,AB= AE,AC= AF,∠BAE= ∠CAF= 90°,判断线段 EF和 AD 的数量关系和位置关系,并加以证明.

答案：
EF = 2AD，EF⊥AD。证明如下：
如图，延长AD到点M，使得DM = AD，连结BM，延长DA与EF相交于点P。

易证△BDM≌△CDA，用倍长中线法即可证明。
∴BM = AC，∠M = ∠CAD．又AC = AF，
∴BM = AF。易知AC//BM，
∴∠BAC + ∠ABM = °．
∵∠BAE = ∠CAF = 90°，
∴∠BAC + ∠EAF = 80°，
∴∠ABM = ∠EAF。
在△ABM和△EAF中，{AB = EA∠ABM = ∠EAFBM = AF}
∴△ABM≌△EAF(SAS)，
∴AM = EF，∠BAM = ∠E．
又AM = AD∠BAM + ∠EAP = ∠BAE = 90°
∴EF = AD∠E + ∠EAP =
∴∠EPA = 90°EF⊥AD归纳总结：此题作为开放型探究问题，通过观察—猜想—证明等一系列探究过程分析主要考查了全等三角形判定和性质难点正确作出辅助线构造全等三角形找到角之间关系

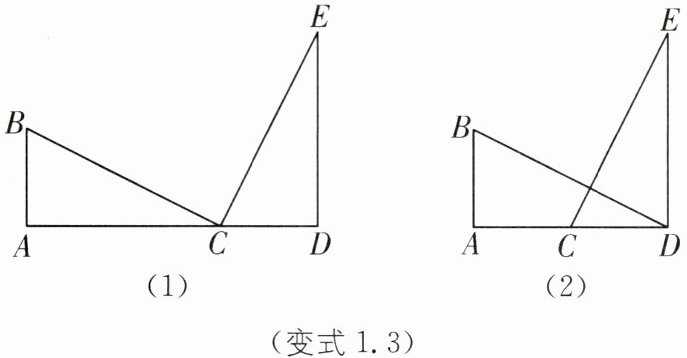
变式 1.3 (1)如图(1),AB⊥AD,ED⊥AD,AB= CD,AC= DE,试说明 BC⊥CE 的理由；(2)如图(2),若△ABC 向右平移,使得点 C 移到点 D 的位置,AB⊥AD,ED⊥AD,AB= CD,AD= DE,探索 BD⊥CE 的结论是否成立,并说明理由.

答案： 【解析】：本题主要考查全等三角形的判定和性质以及垂直的证明。
（1）对于图（1），由于$AB\perp AD$，$ED\perp AD$，所以$\angle A=\angle D=90^\circ$。
在$\triangle ABC$和$\triangle DCE$中，已知$AB=CD$，$\angle A=\angle D$，$AC=DE$，
根据$SAS$（两边及夹角）全等条件，可以得出$\triangle ABC\cong\triangle DCE$。
由于全等三角形的对应角相等，所以$\angle ACB=\angle DEC$。
又因为$\angle D=90^\circ$，所以$\angle DCE+\angle DEC=90^\circ$。
将$\angle ACB=\angle DEC$代入上式，得到$\angle DCE+\angle ACB=90^\circ$。
由于$\angle BCE=180^\circ-(\angle DCE+\angle ACB)$，所以$\angle BCE=90^\circ$，即$BC\perp CE$。
（2）对于图（2），当$\triangle ABC$向右平移使得点C移到点D的位置时，同样由于$AB\perp AD$，$ED\perp AD$，所以$\angle BAC=\angle CDE=90^\circ$。
由于平移不改变图形的形状和大小，所以$AB=CD$，$AC=DE$，且此时$AD=DE$（题目给出）。
在$\triangle ABD$和$\triangle DCE$中，已知$AB=CD$，$\angle BAD=\angle CDE$，$AD=DE$，
根据$SAS$（两边及夹角）全等条件，可以得出$\triangle ABD\cong\triangle DCE$。
由于全等三角形的对应角相等，所以$\angle ADB=\angle DEC$。
延长$BD$交$CE$于点$F$，由于$\angle CDE=90^\circ$，所以$\angle CDF+\angle DEC=90^\circ$。
将$\angle ADB=\angle DEC$代入上式，得到$\angle CDF+\angle ADB=90^\circ$。
由于$\angle DFC=180^\circ-(\angle CDF+\angle ADB)$，所以$\angle DFC=90^\circ$，即$BD\perp CE$。
【答案】：
(1)理由见解析；
(2)成立，理由见解析。