《2025年实验班提优训练八年级数学上册浙教版》

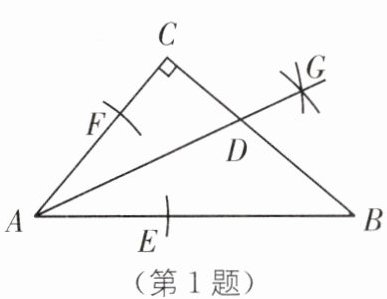
1.(2024·云南普洱期末)如图,在△ABC 中,∠C= 90°,按以下步骤作图:①以点 A 为圆心,小于AC 的长为半径画弧,分别交 AB,AC 于点 E,F;②分别以点 E,F 为圆心,大于$\frac{1}{2}EF$的长为半径画弧,两弧相交于点 G;③作射线 AG交边 BC 于点 D,若 CD= 5,AB= 12,则△ABD 的面积为( ).

A.12
B.30
C.13
D.60

答案：
B [解析]如图,过点 D 作 DH⊥AB 于点 H.

由题意,得 AG 是∠CAB 的平分线.
∵∠C=90°,
∴CD=DH=5.
∵AB=12,
∴S△ABD=$\frac{1}{2}$AB·DH=30. 故选 B.

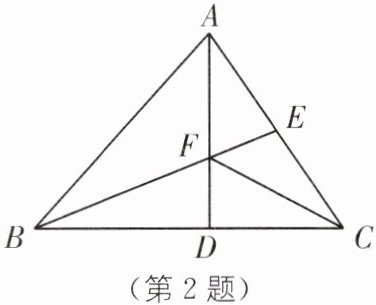
2.(2024·福建莆田期末)如图,在△ABC 中,AD⊥BC 于点 D,BE 为边 AC 上的中线,AD 与 BE 交于点 F,连结 CF.若 CF 平分∠ACB,DF= 3,AC= 10,则△AEF 的面积为( ).

A.30
B.15
C.$\frac{15}{2}$
D.$\frac{15}{4}$

答案：
C [解析]如图,过点 F 作 FG⊥AC 于点 G.

∵AD⊥BC,CF 平分∠ACB,DF=3,
∴FG=DF=3.
∵AC=10,
∴S△ACF=$\frac{1}{2}$AC·FG=$\frac{1}{2}$×10×3=15.
∵BE 为边 AC 上的中线,
∴S△AEF=$\frac{1}{2}$S△ACF=$\frac{15}{2}$. 故选 C.

3.三条公路两两相交,要在该平面内修建一个加油站,使加油站到三条公路的距离都相等,则满足条件的加油站可以建4处.

答案： 4

4. 教材 P51目标与评定 T25·变式 如图,OC 平分∠AOB,DE⊥OA 于点 E,DF⊥OB 于点 F,求证:OD 垂直平分 EF.

答案：
∵OC 平分∠AOB,DE⊥OA 于点 E,DF⊥OB 于点 F,
∴∠DOE=∠DOF,DE=DF,∠OED=∠OFD=90°.
在△ODE 和△ODF 中,$\left\{\begin{array}{l} ∠DOE=∠DOF,\\ ∠OED=∠OFD,\\ DE=DF,\end{array}\right. $
∴△ODE≌△ODF(AAS),
∴∠ODE=∠ODF.
设 OC 交 EF 于点 H,
易证△DEH≌△DFH(SAS),
∴EH=FH,∠DHE=∠DHF=90°,
∴点 O,D 在 EF 的中垂线上,即 OD 垂直平分 EF.

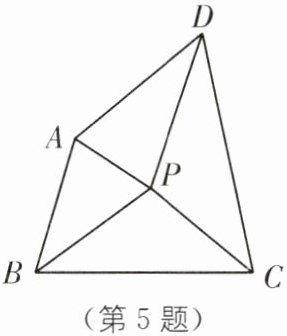
5.(安徽宣城郎溪中学自主招生)如图,四边形 ABCD中,∠A,∠B,∠C,∠D 的平分线恰相交于一点 P (A,P,C 三点不共线),记△APD,△APB,△BPC,△DPC 的面积分别为$S_{1}$,$S_{2}$,$S_{3}$,$S_{4}$,则有( ).

A.$S_{1}+S_{3}= S_{2}+S_{4}$
B.$S_{1}+S_{2}= S_{3}+S_{4}$
C.$S_{1}+S_{4}= S_{2}+S_{3}$
D.$S_{1}= S_{3}$

答案：
A [解析]如图,可将四边形分成 8 个三角形,面积分别是a,a,b,b,c,c,d,d,

则 S₁=a+d,S₂=a+b,S₃=b+c,S₄=c+d,
∴S₁+S₃=a+b+c+d=S₂+S₄. 故选 A.

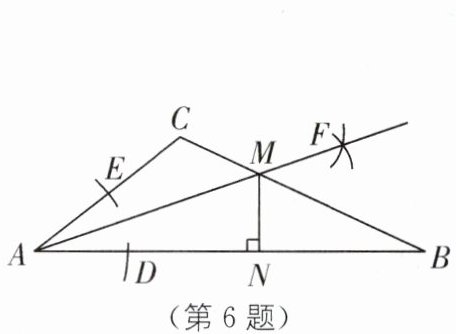
6.如图所示,在△ABC中,按下列步骤作图:
第一步:在 AB,AC 上分别截取 AD,AE,使AD= AE;
第二步:分别以点 D 和点 E 为圆心,适当长(大于 DE 的一半)为半径作圆弧,两弧交于点 F;
第三步:作射线 AF 交 BC 于点 M;
第四步:过点 M 作 MN⊥AB 于点 N.
下列结论一定成立的是(C).

A.CM= MN
B.AC= AN
C.∠CAM= ∠BAM
D.∠CMA= ∠NMA

答案： C [解析]由题意可知,AM 平分∠CAB.
∵∠C 不一定等于 90°,
∴CM≥MN,故 A 选项不正确；
∵∠C 不一定等于 90°,
∴AC 不一定等于 AN,故 B 选项不正确；
∵AM 平分∠CAB,
∴∠CAM=∠BAM,故 C 选项正确；
∵∠C 不一定等于 90°,
∴∠CMA 不一定等于∠NMA,
∴D 选项不正确. 故选 C.

7. 中考新考法 尺规作图 (2024·江苏泰州兴化期末)如图,在△ABC 中,∠A= 110°.
(1)用无刻度的直尺和圆规求作一点 P,使得点 P 到 B,C 两点的距离相等,并且到 AC,BC 两边的距离也相等;(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,若∠ABP= 10°,求∠BPC 的度数.

答案：

(1)如图,点 P 即为所求.

(2)如图,连结 BP,由
(1)可知,BP=CP,∠ACP=∠BCP,
∴∠CBP=∠BCP.
∵∠A+∠ABC+∠ACB=180°,
∴∠A +∠ABP+∠CBP+∠BCP+∠ACP=∠A +∠ABP+3∠BCP=180°.
∵∠A=110°,∠ABP=10°,
∴∠BCP=20°,
∴∠BPC=180°-∠CBP-∠BCP=180°-20°-20°=140°.