《2025年实验班提优训练八年级数学上册浙教版》

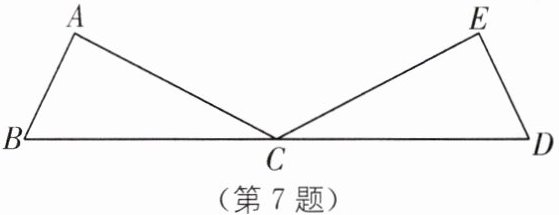
7.(2023·云南中考)如图,C 是 BD 的中点,AB= ED,AC= EC. 求证：△ABC≌△EDC.

答案：
∵C是BD的中点，
∴BC=DC.
在△ABC和△EDC中，AB=ED，AC=EC，BC=DC，
∴△ABC≌△EDC(SSS).

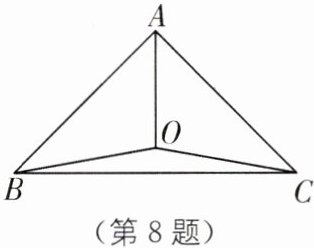
8. 如图,已知 AB= AC,BO= CO,∠BOC= 160°,求∠AOB 的度数.

答案： 在△AOB和△AOC中，AB=AC，AO=AO，BO=CO，
∴△AOB≌△AOC(SSS).
∴∠AOB=∠AOC.
∵∠AOB+∠AOC+∠BOC=360°，∠BOC=160°，
∴∠AOB=∠AOC=100°.

9. 化归思想 两组邻边分别相等的四边形叫作筝形. 如图,在筝形 ABCD 中,AB= AD,BC= DC,AC,BD 相交于点 O.
(1)求证：△ABC≌△ADC；
(2)如果 AC⊥BD,AC= 6,BD= 4,求筝形 ABCD 的面积.

答案：
(1)在△ABC和△ADC中，AB=AD，BC=DC，AC=AC，
∴△ABC≌△ADC(SSS).
(2)
∵AC⊥BD，
∴$S_{四边形ABCD}=S_{△ABC}+S_{△ADC}= \frac{1}{2}AC·BO+ \frac{1}{2}AC·OD= \frac{1}{2}AC·(BO+OD)= \frac{1}{2}AC·BD= \frac{1}{2}×6×4=12.$

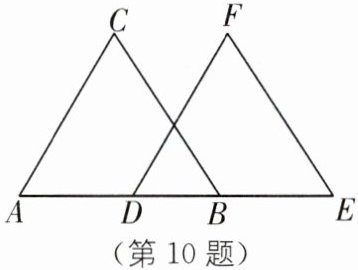
10.(2024·内江中考)如图,点 A,D,B,E 在同一条直线上,AD= BE,AC= DF,BC= EF.
(1)求证：△ABC≌△DEF；
(2)若∠A= 55°,∠E= 45°,求∠F 的度数.

答案：
(1)
∵AD=BE，
∴AD+BD=BE+BD，即AB=DE.
在△ABC和△DEF中，AB=DE，AC=DF，BC=EF，
∴△ABC≌△DEF(SSS).
(2)
∵∠A=55°，∠E=45°，
由
(1)可知，△ABC≌△DEF，
∴∠A=∠FDE=55°，
∴∠F=180°-(∠FDE+∠E)=180°-(55°+45°)=80°.