第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
7. 如图,点 M 是线段 AB 上一点,ED 经过点 M,连结 AE,BD,过点 B 作 BF//AE 交 ED 于点 F,且 EM= FM.
(1)若 AE= 5,求 BF 的长;
(2)若∠AEC= 90°,∠DBF= ∠CAE,求证:CD= FE.
]
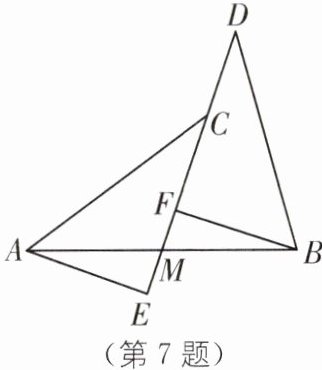
(1)若 AE= 5,求 BF 的长;
(2)若∠AEC= 90°,∠DBF= ∠CAE,求证:CD= FE.
]

答案:
(1)解:
∵BF//AE,
∴∠AEM=∠BFM。在△AEM和△BFM中,∠AEM=∠BFM,EM=FM,∠AME=∠BMF,
∴△AEM≌△BFM(ASA),
∴BF=AE=5。
(2)证明:由
(1)知△AEM≌△BFM,
∴AE=BF。
∵∠AEC=90°,
∴∠AED=90°,又BF//AE,
∴∠BFD=∠AED=90°,
∴∠BFC=∠AEC=90°。在△AEC和△BFC中,∠CAE=∠DBF,AE=BF,∠AEC=∠BFC,
∴△AEC≌△BFC(ASA),
∴EC=FC。
∵ED=EC+CD,EF=FC+CD,
∴CD=FE。
(1)解:
∵BF//AE,
∴∠AEM=∠BFM。在△AEM和△BFM中,∠AEM=∠BFM,EM=FM,∠AME=∠BMF,
∴△AEM≌△BFM(ASA),
∴BF=AE=5。
(2)证明:由
(1)知△AEM≌△BFM,
∴AE=BF。
∵∠AEC=90°,
∴∠AED=90°,又BF//AE,
∴∠BFD=∠AED=90°,
∴∠BFC=∠AEC=90°。在△AEC和△BFC中,∠CAE=∠DBF,AE=BF,∠AEC=∠BFC,
∴△AEC≌△BFC(ASA),
∴EC=FC。
∵ED=EC+CD,EF=FC+CD,
∴CD=FE。
8. 类比思想 如图(1),在等腰直角三角形 ABC 中,∠BAC= 90°,AB= AC,直线 MN 经过点 A,BD⊥MN 于点 D,CE⊥MN 于点 E.
(1)求证:△BAD≌△ACE;
(2)试判断线段 DE,BD,CE 之间的数量关系,并说明理由;
(3)当直线 MN 运动到如图(2)所示位置时,其余条件不变,判断线段 DE,BD,CE 之间的数量关系.
]
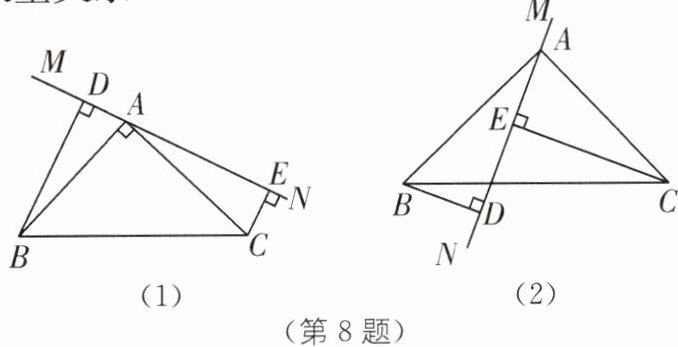
(1)求证:△BAD≌△ACE;
(2)试判断线段 DE,BD,CE 之间的数量关系,并说明理由;
(3)当直线 MN 运动到如图(2)所示位置时,其余条件不变,判断线段 DE,BD,CE 之间的数量关系.
]

答案:
(1)证明:
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥MN,CE⊥MN,
∴∠ADB=∠CEA=90°,∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△BAD和△ACE中,
$\left\{\begin{array}{l} ∠ADB=∠CEA\\ ∠ABD=∠CAE\\ AB=AC\end{array}\right.$,
∴△BAD≌△ACE(AAS);
(2)解:DE=BD+CE,理由如下:
∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=BD+CE;
(3)解:DE=CE-BD,理由如下:
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥MN,CE⊥MN,
∴∠ADB=∠CEA=90°,∠CAE+∠ACE=90°,
∴∠BAD=∠ACE,
在△BAD和△ACE中,
$\left\{\begin{array}{l} ∠ADB=∠CEA\\ ∠BAD=∠ACE\\ AB=AC\end{array}\right.$,
∴△BAD≌△ACE(AAS),
∴BD=AE,AD=CE,
∵DE=AD-AE,
∴DE=CE-BD.
(1)证明:
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥MN,CE⊥MN,
∴∠ADB=∠CEA=90°,∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△BAD和△ACE中,
$\left\{\begin{array}{l} ∠ADB=∠CEA\\ ∠ABD=∠CAE\\ AB=AC\end{array}\right.$,
∴△BAD≌△ACE(AAS);
(2)解:DE=BD+CE,理由如下:
∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=BD+CE;
(3)解:DE=CE-BD,理由如下:
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥MN,CE⊥MN,
∴∠ADB=∠CEA=90°,∠CAE+∠ACE=90°,
∴∠BAD=∠ACE,
在△BAD和△ACE中,
$\left\{\begin{array}{l} ∠ADB=∠CEA\\ ∠BAD=∠ACE\\ AB=AC\end{array}\right.$,
∴△BAD≌△ACE(AAS),
∴BD=AE,AD=CE,
∵DE=AD-AE,
∴DE=CE-BD.
9. 新情境 应用全等测量长度 (2025·山东烟台招远期中)小明同学沿一段笔直的人行道行走,在由 A 处步行到达 B 处的过程中,通过隔离带的空隙 O 刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:如图,AB//OH//CD,相邻两平行线间的距离相等,AC,BD 相交于点 O,OD⊥CD,垂足为 D,已知 AB= 15 米,请根据上述信息求标语 CD 的长度.
]
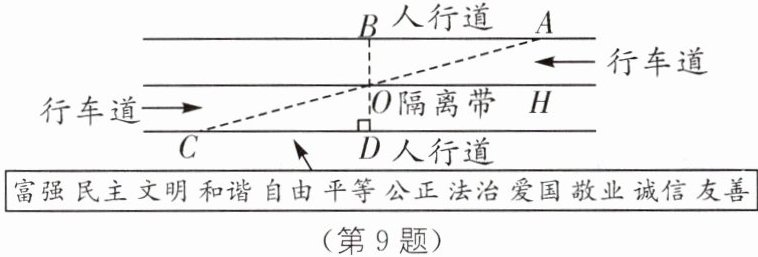
]

答案:
证明:
∵AB//CD,OD⊥CD,
∴OD⊥AB,即∠OAB=∠OCD=90°。
∵相邻两平行线间的距离相等,
∴OD=OE(设OE为O到AB的距离)。
在△OAB和△OCD中,
∠OAB=∠OCD=90°,
∠AOB=∠COD(对顶角相等),
OD=OE=AB边上的高,
∴△OAB≌△OCD(AAS)。
∴CD=AB=15米。
答:标语CD的长度为15米。
∵AB//CD,OD⊥CD,
∴OD⊥AB,即∠OAB=∠OCD=90°。
∵相邻两平行线间的距离相等,
∴OD=OE(设OE为O到AB的距离)。
在△OAB和△OCD中,
∠OAB=∠OCD=90°,
∠AOB=∠COD(对顶角相等),
OD=OE=AB边上的高,
∴△OAB≌△OCD(AAS)。
∴CD=AB=15米。
答:标语CD的长度为15米。
10. (2024·牡丹江中考)如图,在△ABC 中,D 是 AB 上一点,CF//AB,D,E,F 三点共线,请添加一个条件
AD=CF
,使得 AE= CE.(只添一种情况即可)
答案:
【解析】:本题可根据全等三角形的判定定理来添加条件,使得$\triangle ADE$和$\triangle CFE$全等,进而得到$AE = CE$。
已知$CF// AB$,根据两直线平行,内错角相等,可得$\angle ADE=\angle CFE$,$\angle DAE=\angle FCE$。
此时在$\triangle ADE$和$\triangle CFE$中,已经有两组角对应相等,根据全等三角形的判定定理“$AAS$”(两角及其中一角的对边对应相等的两个三角形全等)或“$ASA$”(两角及其夹边对应相等的两个三角形全等),可添加一组对应边相等,比如$AD = CF$或$\angle AED=\angle CEF$(对顶角相等,添加此条件可利用“$ASA$”判定全等)或$\angle DAE=\angle FCE$(已知平行已得,也可作为已知条件利用其他方式推导全等,这里主要考虑添加边或另一组角的情况),这里我们选择添加$AD = CF$来使得两个三角形全等。
当$AD = CF$时,在$\triangle ADE$和$\triangle CFE$中:
$\begin{cases}\angle ADE=\angle CFE\\\angle DAE=\angle FCE\\AD = CF\end{cases}$
根据“$AAS$”可判定$\triangle ADE\cong\triangle CFE$,全等三角形对应边相等,所以$AE = CE$。
【答案】:$AD = CF$(答案不唯一)。
已知$CF// AB$,根据两直线平行,内错角相等,可得$\angle ADE=\angle CFE$,$\angle DAE=\angle FCE$。
此时在$\triangle ADE$和$\triangle CFE$中,已经有两组角对应相等,根据全等三角形的判定定理“$AAS$”(两角及其中一角的对边对应相等的两个三角形全等)或“$ASA$”(两角及其夹边对应相等的两个三角形全等),可添加一组对应边相等,比如$AD = CF$或$\angle AED=\angle CEF$(对顶角相等,添加此条件可利用“$ASA$”判定全等)或$\angle DAE=\angle FCE$(已知平行已得,也可作为已知条件利用其他方式推导全等,这里主要考虑添加边或另一组角的情况),这里我们选择添加$AD = CF$来使得两个三角形全等。
当$AD = CF$时,在$\triangle ADE$和$\triangle CFE$中:
$\begin{cases}\angle ADE=\angle CFE\\\angle DAE=\angle FCE\\AD = CF\end{cases}$
根据“$AAS$”可判定$\triangle ADE\cong\triangle CFE$,全等三角形对应边相等,所以$AE = CE$。
【答案】:$AD = CF$(答案不唯一)。
查看更多完整答案,请扫码查看


