《2025年实验班提优训练八年级数学上册浙教版》

1.(温州中学自主招生)有以下关于x,y的等式：①$x+2y= 0$；②$x^{2}+y^{2}= 2$；③$x= |y|$；④$xy= 1$,其中y是x的函数的有(B).
A.1个
B.2个
C.3个
D.4个

答案： B [解析]①x+2y=0,则y=-$\frac{1}{2}$x,对于x的每一个确定的值,y都有唯一确定的值与之对应,
∴y是x的函数；②$x^2+y^2=2$,对于x的每一个确定的值,y的值不唯一,
∴y不是x的函数；③x=|y|,对于x的每一个确定的值,y的值不唯一,
∴y不是x的函数；④xy=1,对于x的每一个确定的值,y都有唯一确定的值与之对应,
∴y是x的函数.综上所述,y是x的函数的有①④,共2个.故选B.

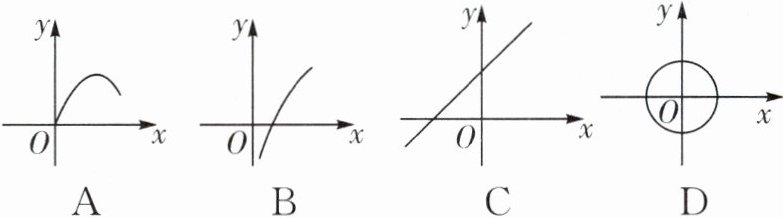
2.(2025·湖州长兴期末)下列各曲线表示的y与x之间的关系中,y不是x的函数的是(D).

A
B
C D

答案： D [解析]A.对于自变量x的每一个值,因变量y都有唯一确定的值与它对应,所以y是x的函数,故A不符合题意；B.对于自变量x的每一个值,因变量y都有唯一确定的值与它对应,所以y是x的函数,故B不符合题意；C.对于自变量x的每一个值,因变量y都有唯一确定的值与它对应,所以y是x的函数,故C不符合题意；D.对于自变量x的每一个值,因变量y不是都有唯一的值与它对应,所以y不是x的函数,故D符合题意.故选D.

3. 教材P158作业题T2·变式 当$x= -2$时,函数$y= \sqrt{4x+9}$的函数值为1.

答案： 1 [解析]当x=-2时,y=$\sqrt{4x+9}$=$\sqrt{4×(-2)+9}$=$\sqrt{1}$=1.

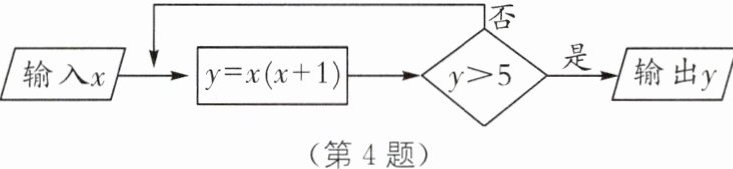
4. 如图所示是关于变量x,y的程序计算,若开始输入的x值为2,则最后输出y的值为6.

(第4题)

答案： 6 [解析]由题意可得,当x=2时,y=x(x+1)=2×(2+1)=6＞5,
∴输出y=6.

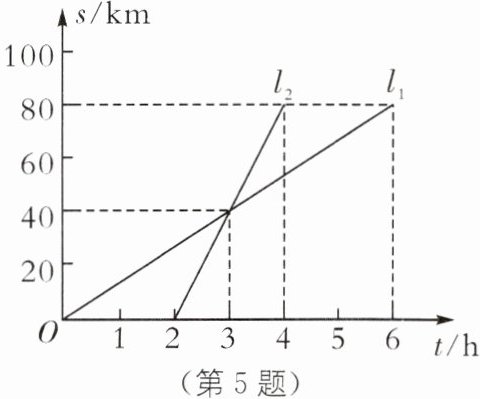
5.(2025·陕西西安鄠邑区期末)已知A,B两地相距80 km,甲、乙两人沿同一条道路从A地到达B地.如图,$l_{1},l_{2}$分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.
(1)在甲出发3h时,两人相遇,这时他们离开A地40km；
(2)求甲、乙的速度；
(2)甲的速度是$\frac{80}{6}$=$\frac{40}{3}$(km/h),乙的速度是$\frac{80}{4-2}$=40(km/h).
(3)乙从A地出发2h时到达B地.

(第5题)

答案：
(1)3 40
(2)甲的速度是$\frac{80}{6}$=$\frac{40}{3}$(km/h),乙的速度是$\frac{80}{4-2}$=40(km/h).
(3)2

6.(安徽自主招生)$[x]$表示不大于x的最大整数,学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表,那么各班可推选代表人数y与该班人数x之间的函数关系用取整函数$y= [x]$可以表示为(B).
A.$y= [\frac{x}{10}]$
B.$y= [\frac{x+3}{10}]$
C.$y= [\frac{x+4}{10}]$
D.$y= [\frac{x+5}{10}]$

答案： B [解析]根据题意,得到余数为7,8,9时可以增选一名代表,也就是要进一位,所以最小应该加3,用取整函数表示为y=$\left\lfloor \frac{x+3}{10} \right\rfloor$.故选B.

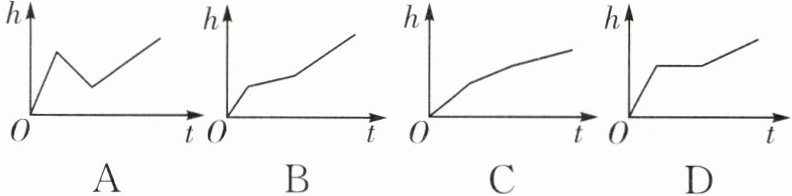
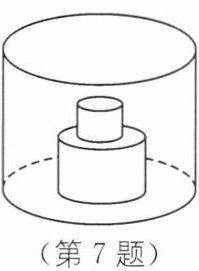
7. 建模思想(2025·四川模拟)如图,一个圆柱形水槽底部叠放两个底面半径不等的实心圆柱,向水槽匀速注水.下列图象能大致反映水槽中水的深度h与注水时间t的函数关系的是(C).


A
B
C D

(第7题) (第8题)

答案： C [解析]下层圆柱底面半径大,水面上升块,上层圆柱底面半径稍小,水面上升稍慢,再往上则水面上升更慢,所以对应图象是第一段比较陡,第二段比第一段缓,第三段比第二段缓.故选C.

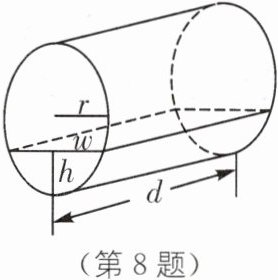
8. 新情境 加油站储油罐 如图是某加油站地下圆柱形储油罐示意图,已知储油罐长度为d,截面半径为r(d,r为常量),油面高度为h,油面宽度为w,油量为v(h,w,v为变量),则下面四个结论：①w是v的函数；②v是w的函数；③h是w的函数；④w是h的函数.其中正确结论的序号是______①④.

答案： ①④ [解析]根据圆柱的体积公式的实际应用,油量为v,会影响油面高度h,从而影响油面的宽度w,对于①,w是v的函数,由于v确定,故h确定,w就确定,故①正确；对于②,v是w的函数,由于w确定,h有两个(上下对称),所以v有两个,故与函数的定义相矛盾,不是函数,故②错误；对于③,h是w的函数,同②,w确定,所以有两个h(上下对称),故与函数的定义相矛盾,不是函数,故③错误；对于④,w是h的函数,h确定,则w确定,故④正确.故①④正确.

9. 跨学科 弹簧 在一次实验中,小达同学把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧长度y与所挂物体质量的一组对应值.

(1)上表反映了哪两个变量之间的关系？并指出谁是自变量,谁是因变量.上表反映了弹簧长度y与所挂物体质量x之间的关系，所挂物体质量x是自变量，弹簧长度y是因变量.
(2)当悬挂物体的重量为4千克时,弹簧长26 cm；不挂重物时弹簧长18 cm.
(3)弹簧长度y与所挂物体质量x之间的关系可以用式子表示为y=18+2x.
(4)求挂12 kg物体时弹簧长度及弹簧长40 cm时所挂物体的重量(均在弹簧弹性限度范围内).当x=12时,y=18+2×12=42,当y=40时,40=18+2x,解得x=11.故挂12千克物体时弹簧长度为42 cm,弹簧长40 cm时所挂物体的质量是11 kg.

答案：
(1)上表反映了弹簧长度y与所挂物体质量x之间的关系，所挂物体质量x是自变量，弹簧长度y是因变量.
(2)26 cm 18 cm [解析]从表格中可以得到：当悬挂物体的质量为4千克时,弹簧的长度为26 cm；不挂重物时,也就是x=0时,弹簧长为18 cm.
(3)y=18+2x [解析]观察表格发现,所挂物体的质量增加1 kg,弹簧就伸长2 cm,
∴y=18+2x.
(4)当x=12时,y=18+2×12=42,当y=40时,40=18+2x,解得x=11.故挂12千克物体时弹簧长度为42 cm,弹簧长40 cm时所挂物体的质量是11 kg.