第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
10. A,B,C,D,E五名学生猜自己的数学成绩:
A说:“如果我得优,那么B也得优.”
B说:“如果我得优,那么C也得优.”
C说:“如果我得优,那么D也得优.”
D说:“如果我得优,那么E也得优.”
大家都没有说错,但只有三个人得优. 请问:得优的是哪三个人?
A说:“如果我得优,那么B也得优.”
B说:“如果我得优,那么C也得优.”
C说:“如果我得优,那么D也得优.”
D说:“如果我得优,那么E也得优.”
大家都没有说错,但只有三个人得优. 请问:得优的是哪三个人?
答案:
C,D,E得优
11. 中考新考法 满足结论的条件开放 在△ABC中,BD,CE相交于点F,试在下列设定的条件中选择若干个条件作为题设,另一个条件作为结论,组合成一个真命题,并说明理由.
①∠A= α;
②BD,CE分别是∠ABC,∠ACB的平分线;
③BD,CE是△ABC的两条高线;
④∠BFC= 90°+1/2α;
⑤∠BFC= 180°-α.
①∠A= α;
②BD,CE分别是∠ABC,∠ACB的平分线;
③BD,CE是△ABC的两条高线;
④∠BFC= 90°+1/2α;
⑤∠BFC= 180°-α.
答案:
答案不唯一,合理即可.条件:∠A=α,BD,CE是△ABC 的两条高线,如图 结论:∠BFC=180°-α. 理由如下:
结论:∠BFC=180°-α. 理由如下:
∵BD,CE是△ABC的两条高线,
∴∠ADB=90°,∠AEC=90°.
∴∠ABD=∠ACE=180°-90°-∠A=90°-α.
∴∠FBC+∠FCB=180°-∠ABD-∠ACE-∠A=α.
∴∠BFC=180°-(∠FBC+∠FCB)=180°-α.
答案不唯一,合理即可.条件:∠A=α,BD,CE是△ABC 的两条高线,如图
 结论:∠BFC=180°-α. 理由如下:
结论:∠BFC=180°-α. 理由如下:∵BD,CE是△ABC的两条高线,
∴∠ADB=90°,∠AEC=90°.
∴∠ABD=∠ACE=180°-90°-∠A=90°-α.
∴∠FBC+∠FCB=180°-∠ABD-∠ACE-∠A=α.
∴∠BFC=180°-(∠FBC+∠FCB)=180°-α.
12. 假设推理思想 甲和乙玩一个猜数游戏,规则如下:已知五张纸牌上分别写有1,2,3,4,5五个数字,现甲、乙两人分别从中各自随机抽取一张,然后根据自己手中的数推测谁手上的数更大. 甲看了看自己手中的数,想了想 说:我不知道谁手中的数更大;乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大. 假设甲、乙所作出的推理都是正确的,那么乙手中的数是
3
.
答案:
3 [解析]五张纸牌上分别写有1,2,3,4,5五个数字.
∵甲看了看自己手中的数,想了想说:我不知道谁手中的数更大,
∴甲手中的数可能为2,3,4.
∵乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大,
∴乙手中的数不可能是2,4,只能是3.
∵甲看了看自己手中的数,想了想说:我不知道谁手中的数更大,
∴甲手中的数可能为2,3,4.
∵乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大,
∴乙手中的数不可能是2,4,只能是3.
13. 阅读下面材料:
判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
例如要判断命题“相等的角是对顶角”是假命题,可以举出如下反例:
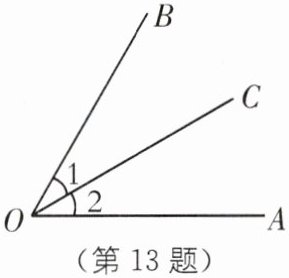
如图,OC是∠AOB的平分线,∠1= ∠2,但它们不是对顶角.
请你举出一个反例说明命题“如果两个角的两边分别平行,那么这两个角相等”是假命题.(要求:画出相应的图形,并用文字语言或符号语言表述所举反例)
判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
例如要判断命题“相等的角是对顶角”是假命题,可以举出如下反例:
如图,OC是∠AOB的平分线,∠1= ∠2,但它们不是对顶角.
请你举出一个反例说明命题“如果两个角的两边分别平行,那么这两个角相等”是假命题.(要求:画出相应的图形,并用文字语言或符号语言表述所举反例)

答案:
如图,∠1和∠2的两边分别平行,∠1+∠2=180°,所以如果两个角的两边分别平行,那么这两个角相等或互补.
如图,∠1和∠2的两边分别平行,∠1+∠2=180°,所以如果两个角的两边分别平行,那么这两个角相等或互补.

查看更多完整答案,请扫码查看


