《2025年实验班提优训练八年级数学上册浙教版》

1.(2024·杭州竺可桢中学期中)下列条件中,不能判断一个三角形是直角三角形的是(C).
A.三个角的比为1:2:3
B.三条边满足关系$a^{2}= b^{2}-c^{2}$
C.三条边的比为1:2:3
D.三个角满足关系$\angle B+\angle C= \angle A$

答案： C　[解析]A.三个角的比为1:2:3,设最小的角为x,则x+2x+3x=180°,x=30°,3x=90°,故正确;
B.三条边满足关系a²=b²−c²,故正确;
C.三条边的比为1:2:3,1²+2²≠3²,故错误;
D.三个角满足关系∠B+∠C=∠A,则∠A为90°,故正确.故选C.

2.(2024·金华金东区期中)下列各组线段中的三个长度：①9,12,15；②5,12,13；③$3^{2},4^{2},5^{2}$；④1,2,$\sqrt{3}$.其中可以构成直角三角形的有(B).
A.4组
B.3组
C.2组
D.1组

答案： B　[解析]①9²+12²=15²,故可以构成直角三角形;
②5²+12²=13²,故可以构成直角三角形;
③(3²)²+(4²)²≠(5²)²,故不可以构成直角三角形;
④1²+( $\sqrt{3}$)²=2²,故可以构成直角三角形.
综上，符合题意的有3组.故选B.

3. 一个三角形的三边长分别为5,12,13,则这个三角形最长边上的中线为$\frac{13}{2}$.

答案： $\frac{13}{2}$　[解析]
∵三角形的三边长分别为5,12,13，且5²+12²=13²,
∴此三角形为直角三角形，且13为直角三角形的斜边.
∵三角形斜边上的中线是斜边的一半,
→直角三角形斜边中线定理
∴三角形最长边上的中线为$\frac{13}{2}$.

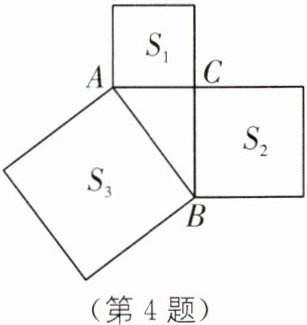
4. 教材P84作业题T2·变式 如图,在$\triangle ABC$中,以$\triangle ABC各边为边在\triangle ABC$外作正方形,$S_{1},S_{2},S_{3}$分别表示这三个正方形的面积,$S_{1}= 81$,$S_{2}= 144$,$S_{3}= 225$,则$\triangle ABC$是______三角形.
]

直角

答案： 直角　[解析]由题意,得AC²=S₁=81,BC²=S₂=144,AB²=S₃=225,所以AC²+BC²=AB²,所以△ABC是直角三角形.

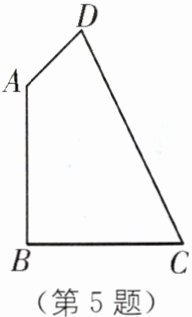
5. 如图,在四边形ABCD中,$AB= BC= 2$,$CD= 3$,$DA= 1$,且$\angle B= 90^{\circ}$,求$\angle DAB$的度数.
]

答案： 连结AC.
∵∠B=90°,AB=BC=2,
∴AC²=AB²+BC²=8,∠BAC=45°.
又CD=3,DA=1,
∴AC²+DA²=8+1=9,CD²=9,
∴AC²+DA²=CD².
∴△ACD是直角三角形,∠CAD=90°
→勾股定理的逆定理
∴∠DAB=45°+90°=135°.

下列命题：①如果a,b,c为一组勾股数,那么5a,5b,5c仍是勾股数；②如果直角三角形的两边是3,4,那么另一边必是5；③如果一个三角形的三边是5,13,14,那么此三角形必是直角三角形；④一个等腰直角三角形的三边是a,b,c($a＞b= c$),那么$a^{2}:b^{2}:c^{2}= 2:1:1$.其中正确的是(A).
A.①④
B.①③
C.①②
D.②④

答案： A　[解析]①
∵(5a)²+(5b)²=25a²+25b²=25(a²+b²)=25c²=(5c)²,而5a,5b,5c一定是正整数,
∴5a,5b,5c仍是勾股数，故①符合题意;
②如果直角三角形的两边是3,4,则另一边的长可能为$\sqrt{4²−3²}$=$\sqrt{7}$，且符合三角形的两边之和大于第三边，故②不符合题意;
③5²+13²=25+169=194≠14²,故③不符合题意;
④
∵一个等腰直角三角形的三边a,b,c满足a＞b=c,
∴a²=b²+c²=b²+b²=2b²=2c²,
即a²:b²:c²=2:1:1,故④符合题意.故选A.
归纳总结　本题主要考查了勾股数和直角三角形的性质，正确掌握勾股数的定义和直角三角形的性质是解题的关键.

7.(2025·福建漳州期中)如图,在四边形ABCD中,AC,BD相交于点O,且$AC\perp BD$,若$AD= 2$,$BC= 4$,则$AB^{2}+CD^{2}$的值为(C).
A.8
B.14
C.20
D.26
]

答案： C　[解析]
∵AC⊥BD,
∴AB²=AO²+BO²,CD²=OC²+OD²,BC²=BO²+CO²,AD²=OA²+OD²,
∴AB²+CD²=BC²+AD².
∵AD=2,BC=4,
∴AB²+CD²=4²+2²=20.故选C.

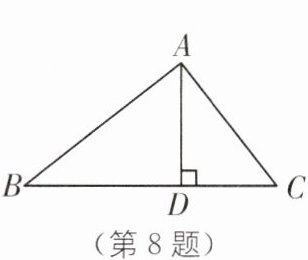
8. 如图,在$\triangle ABC$中,$AD\perp BC$于点D,若$AB= 4\ \text{cm}$,$BC= 5\ \text{cm}$,$AC= 3\ \text{cm}$,则线段AD的长是$\frac{12}{5}$cm.

答案： $\frac{12}{5}$cm　[解析]
∵AB=4cm,BC=5cm,AC=3cm,
∴BC²=AB²+AC²,
∴△ABC为直角三角形，
∴∠BAC=90°.
∵AD⊥BC于点D,
∴S△ABC=$\frac{1}{2}$BC·AD=$\frac{1}{2}$AB·AC,
∴$\frac{1}{2}$×5×AD=$\frac{1}{2}$×4×3,
∴AD=$\frac{12}{5}$cm.

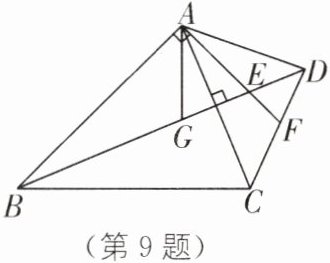
9.(2025·丽水期末改编)如图,在四边形ABCD中,对角线$AC\perp BD$,F为CD上一点,连结AF交BD于点E,$AF\perp AB$,已知$\angle BAG= \angle ABC= 45^{\circ}$,且$BC+AG= \sqrt{2}$.
(1)AB的长是______；
(2)若$AE= 2EF$,$\angle AGD+\angle BCD= 180^{\circ}$,则$AF= $______.
]

答案：

(1)1 ［解析］如图,延长AF,BC交于点H.

∵AF⊥AB,
∴∠BAH=90°.
∵∠ABC=45°,
∴△ABH是等腰直角三角形，
∴∠AHB=45°=∠BAG,AH=AB.
∵AC⊥BD,
∴∠CAH=∠ABG=90°−∠AEG,
在△ABG和△HAC中,$\left\{\begin{array}{l} ∠BAG=∠AHC,\\ AB=HA,\\ ∠ABG=∠HAC,\end{array}\right. $
∴△ABG≌△HAC(ASA),
∴CH=AG.
∵BC+AG=$\sqrt{2}$,
∴BC+CH=BH=$\sqrt{2}$
在Rt△ABH中,AB²+AH²=BH²,
即2AB²=2,
∴AB=1.
(2)$\frac{3}{5}$　[解析]
∵∠AGD+∠BCD=180°,∠FCH+∠BCD=180°,
∴∠AGD=∠FCH.
∵∠BAG=45°,
∴∠EAG=45°=∠FHC.
在△AGE和△HCF中,$\left\{\begin{array}{l} ∠EAG=∠FHC,\\ AG=HC,\\ ∠AGE=∠HCF,\end{array}\right. $
∴△AGE≌△HCF(ASA),
∴FH=AE,
设EF=x,则FH=AE=2x,
∴AH=AE+EF+FH=5x=1,解得x=$\frac{1}{5}$,
∴AF=AE+EF=3x=$\frac{3}{5}$.

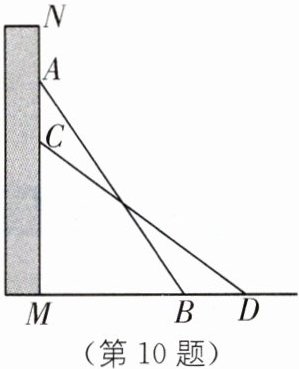
10. 梯子模型 如图,墙面MN与地面DM垂直,把一个长为10 m的梯子AB斜靠在墙面上,测得$BM= 6\ \text{m}$,梯子沿墙面下滑到CD位置,测得$\angle ABM= \angle DCM$.求梯子下滑的距离AC.
]

答案： 在Rt△ABM中,BM=6m,AB=10m,
∴AM=$\sqrt{AB²−BM²}$=$\sqrt{10²−6²}$=8(m).
在△ABM和△DCM中,$\left\{\begin{array}{l} ∠AMB=∠DMC,\\ ∠ABM=∠DCM,\\ AB=DC,\end{array}\right. $
∴△ABM≌△DCM(AAS),
∴BM=CM=6m,
∴AC=AM−CM=2(m),
即梯子下滑的距离AC是2m.