第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
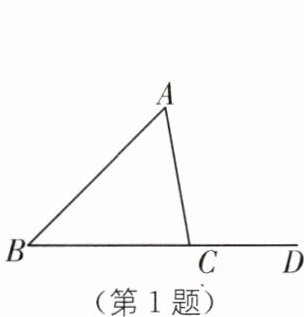
1.(2025·湖北孝感汉川期中)如图,在△ABC 中,∠A= 55°,∠B= 45°,则∠ACD 的度数为(
A.110°
B.100°
C.55°
D.45°
B
).
A.110°
B.100°
C.55°
D.45°
答案:
B
2. 教材 P23课内练习 T1·变式 如图,在△ABC 中,∠C= 90°,AD 是∠BAC 的平分线,若∠ADC= 65°,则∠BAC 的大小为(
A.35°
B.50°
C.65°
D.70°
B
).A.35°
B.50°
C.65°
D.70°
答案:
B [解析]
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC.
∵∠ADC是△ABD的外角,∠ADC=65°,
∴∠B+$\frac{1}{2}$∠BAC=65°①.
∵∠C=90°,
∴∠B+∠BAC=90°②,由②−①,得$\frac{1}{2}$∠BAC=25°,
∴∠BAC=50°.故选B.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC.
∵∠ADC是△ABD的外角,∠ADC=65°,
∴∠B+$\frac{1}{2}$∠BAC=65°①.
∵∠C=90°,
∴∠B+∠BAC=90°②,由②−①,得$\frac{1}{2}$∠BAC=25°,
∴∠BAC=50°.故选B.
3.(2025·广东深圳福田区期末)如图,直线a//b,射线 AB 分别交直线 a,b 于点 B,C,点 D 在直线 a 上,若∠A= 30°,∠1= 50°,则∠2 的度数为(

A.20°
B.30°
C.50°
D.80°
A
).
A.20°
B.30°
C.50°
D.80°
答案:
A [解析]
∵a//b,
∴∠1=∠DBC=50°.
∴∠2=∠DBC−∠A=50°−30°=20°.故选A.
∵a//b,
∴∠1=∠DBC=50°.
∴∠2=∠DBC−∠A=50°−30°=20°.故选A.
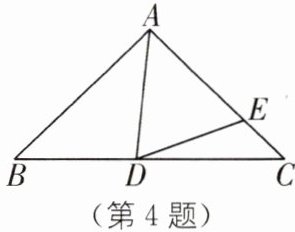
4. 如图,在△ABC 中,∠B= ∠C,∠BAD= 40°,且∠ADE= ∠AED,求∠CDE 的度数.

答案:
由三角形的外角的性质,得∠ADE+∠CDE=∠B+∠BAD,∠AED=∠C+∠CDE.又∠ADE=∠AED,
∴∠C+2∠CDE=∠B+∠BAD.又∠B=∠C,
∴∠BAD=2∠CDE.
∵∠BAD=40°,
∴∠CDE=20°.
∴∠C+2∠CDE=∠B+∠BAD.又∠B=∠C,
∴∠BAD=2∠CDE.
∵∠BAD=40°,
∴∠CDE=20°.
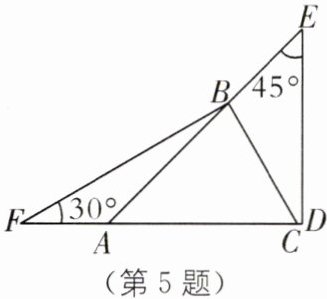
5.(2025·四川绵阳游仙区期中)将一副三角板按照如图方式摆放,则∠CBE 的度数为(
A.90°
B.100°
C.105°
D.110°
C
).
A.90°
B.100°
C.105°
D.110°
答案:
C
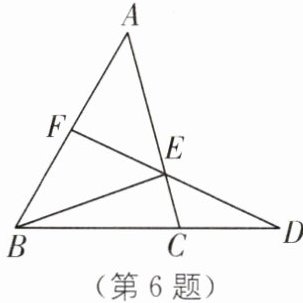
6.(2024·陕西渭南蒲城期末)如图,在△ABC 中,F,E 分别是 AB,AC 上两点,连结 FE 并延长交 BC 的延长线于点 D,若∠A= 45°,∠ABC= 60°,∠D= 25°,则∠AED= ( ).
A.105°
B.85°
C.120°
D.130°

A.105°
B.85°
C.120°
D.130°
答案:
D [解析]
∵∠A=45°,∠ABC=60°,∠ACD是△ABC 的外角,
∴∠ACD=∠A+∠ABC=105°.
∵∠D=25°,∠AED是△CDE的外角,
∴∠AED=∠D+∠ACD=130°.故选D.一题多解 如图,连结BE并延长,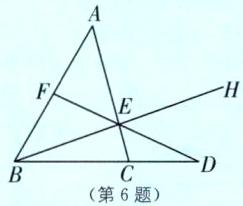
∵∠A=45°,∠AEH是△ABE的外角,
∴∠AEH=∠A+∠ABE=45°+∠ABE,
∵∠D=25°,∠DEH是△BDE的外角,
∴∠DEH=∠D+∠CBE=25°+∠CBE,
∴∠AED=∠AEH+∠DEH=45°+∠ABE+25°+∠CBE,
∵∠ABE+∠CBE=∠ABC=60°,
∴∠AED=45°+25°+60°=130°,
D [解析]
∵∠A=45°,∠ABC=60°,∠ACD是△ABC 的外角,
∴∠ACD=∠A+∠ABC=105°.
∵∠D=25°,∠AED是△CDE的外角,
∴∠AED=∠D+∠ACD=130°.故选D.一题多解 如图,连结BE并延长,

∵∠A=45°,∠AEH是△ABE的外角,
∴∠AEH=∠A+∠ABE=45°+∠ABE,
∵∠D=25°,∠DEH是△BDE的外角,
∴∠DEH=∠D+∠CBE=25°+∠CBE,
∴∠AED=∠AEH+∠DEH=45°+∠ABE+25°+∠CBE,
∵∠ABE+∠CBE=∠ABC=60°,
∴∠AED=45°+25°+60°=130°,
7.(福建福州八中自主招生)一副三角板如图放置,若∠1= 90°,则∠2 的度数为______.
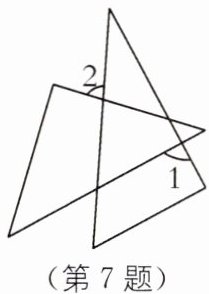

答案:
75° [解析]如图,由题意,得∠B=30°,∠A=45°.
∵∠1=90°,
∴∠A+∠3=90°,
∴∠3=45°,
∴∠4=45°.
∵∠B=30°,
∴∠2=45°+30°=75°,
75° [解析]如图,由题意,得∠B=30°,∠A=45°.
∵∠1=90°,
∴∠A+∠3=90°,
∴∠3=45°,
∴∠4=45°.
∵∠B=30°,
∴∠2=45°+30°=75°,

8. 如图,∠ABC= ∠ACB,AD,BD,CD 分别平分△ABC 的外角∠EAC,内角∠ABC,外角∠ACF,以下结论:①AD//BC;②∠ACB= 2∠ADB;③∠ADC= 90°-∠ABC;④∠BDC= 1/2∠BAC.其中正确的结论有______

①②④
(填序号).
答案:
①②④ [解析]
∵AD平分∠EAC,
∴∠EAC=2∠EAD.
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD//BC,故①正确;
∵AD//BC,
∴∠ADB=∠DBC.
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ACB=∠ABC=2∠DBC,
∴∠ACB=2∠ADB,故②正确;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=$\frac{1}{2}$∠EAC,∠DCA=$\frac{1}{2}$∠ACF,
∵∠EAC=∠ABC+∠ACB,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°−(∠DAC+∠ACD)=180°−$\frac{1}{2}$(∠EAC+∠ACF)=180°−$\frac{1}{2}$(∠ABC+∠ACB+∠ABC+∠BAC)=180°−$\frac{1}{2}$(180°+∠ABC)=90°−$\frac{1}{2}$∠ABC,故③错误;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,故④正确
∵AD平分∠EAC,
∴∠EAC=2∠EAD.
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD//BC,故①正确;
∵AD//BC,
∴∠ADB=∠DBC.
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ACB=∠ABC=2∠DBC,
∴∠ACB=2∠ADB,故②正确;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=$\frac{1}{2}$∠EAC,∠DCA=$\frac{1}{2}$∠ACF,
∵∠EAC=∠ABC+∠ACB,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°−(∠DAC+∠ACD)=180°−$\frac{1}{2}$(∠EAC+∠ACF)=180°−$\frac{1}{2}$(∠ABC+∠ACB+∠ABC+∠BAC)=180°−$\frac{1}{2}$(180°+∠ABC)=90°−$\frac{1}{2}$∠ABC,故③错误;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,故④正确
9.(2025·四川眉山东坡区期末)如图,∠ABC= ∠ACB,BD,CD 分别平分△ABC 的内角∠ABC,外角∠ACP,BE 平分外角∠MBC 交 DC 的延长线于点 E,以下结论:①∠BDE= 1/2∠BAC;②DB⊥BE;③∠BDC+∠ABC= 90°;④∠BAC+2∠BEC= 180°.其中正确的结论有______
①②③④
(填序号).
答案:
①②③④ [解析]①
∵BD,CD分别平分△ABC的内角∠ABC,外角∠ACP,BE平分外角∠MBC交DC的延长线于点E,
∴∠ABC=2∠DBC=2∠ABD,∠ACP=2∠DCP=2∠DCA,∠MBC=2∠CBE=2∠MBE.
∵∠DCP=∠BDC+∠DBC,∠ACP=2∠DCP=∠BAC+∠ABC=∠BAC+2∠DBC,
∴2(∠BDC+∠DBC)=∠BAC+2∠DBC,
∴∠BDE=$\frac{1}{2}$∠BAC,故①正确;②
∵∠DBE=∠DBC+∠EBC=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠MBC=$\frac{1}{2}$×180°=90°,
∴EB⊥DB,故②正确;③
∵∠ABC=∠ACB,
∴∠BAC+2∠ABC=180°,
∴$\frac{1}{2}$∠BAC+∠ABC=90°.
∵∠BDC=$\frac{1}{2}$∠BAC,
∴∠BDC+∠ABC=90°,故③正确;④
∵∠DBE=90°,
∴∠BDE+∠BEC=90°.
∵∠BDE=$\frac{1}{2}$∠BAC,
∴$\frac{1}{2}$∠BAC+∠BEC=90°,
∴∠BAC+2∠BEC=180°,故④正确
∵BD,CD分别平分△ABC的内角∠ABC,外角∠ACP,BE平分外角∠MBC交DC的延长线于点E,
∴∠ABC=2∠DBC=2∠ABD,∠ACP=2∠DCP=2∠DCA,∠MBC=2∠CBE=2∠MBE.
∵∠DCP=∠BDC+∠DBC,∠ACP=2∠DCP=∠BAC+∠ABC=∠BAC+2∠DBC,
∴2(∠BDC+∠DBC)=∠BAC+2∠DBC,
∴∠BDE=$\frac{1}{2}$∠BAC,故①正确;②
∵∠DBE=∠DBC+∠EBC=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠MBC=$\frac{1}{2}$×180°=90°,
∴EB⊥DB,故②正确;③
∵∠ABC=∠ACB,
∴∠BAC+2∠ABC=180°,
∴$\frac{1}{2}$∠BAC+∠ABC=90°.
∵∠BDC=$\frac{1}{2}$∠BAC,
∴∠BDC+∠ABC=90°,故③正确;④
∵∠DBE=90°,
∴∠BDE+∠BEC=90°.
∵∠BDE=$\frac{1}{2}$∠BAC,
∴$\frac{1}{2}$∠BAC+∠BEC=90°,
∴∠BAC+2∠BEC=180°,故④正确
查看更多完整答案,请扫码查看


