第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 如图,直线$l_{1}// l_{2}$,$l_{3}\perp l_{4}$,$\angle 1= 42^{\circ}$,那么$\angle 2$的度数是( ).

A.$21^{\circ}$
B.$24^{\circ}$
C.$42^{\circ}$
D.$48^{\circ}$

A.$21^{\circ}$
B.$24^{\circ}$
C.$42^{\circ}$
D.$48^{\circ}$
答案:
D [解析]如图.

∵l₁//l₂,l₃⊥l₄,∠1=42°,
∴∠4=90°,∠3=∠1=42°,
∴∠2=180°−∠3−∠4=48°.故选D.
D [解析]如图.

∵l₁//l₂,l₃⊥l₄,∠1=42°,
∴∠4=90°,∠3=∠1=42°,
∴∠2=180°−∠3−∠4=48°.故选D.
2. 教材 P21 作业题 T3·变式 如图,$\angle 1= \angle 2= 65^{\circ}$,$\angle 3= 35^{\circ}$,则下列结论错误的是(
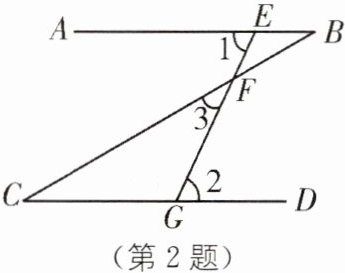
A.$AB// CD$
B.$\angle B= 30^{\circ}$
C.$\angle C+\angle 2= \angle EFC$
D.$CG>FG$
C
).
A.$AB// CD$
B.$\angle B= 30^{\circ}$
C.$\angle C+\angle 2= \angle EFC$
D.$CG>FG$
答案:
C [解析]由∠1=∠2=65°,根据内错角相等,两直线平行,可得AB//CD,故A选项正确;
∵∠3和∠BFE互为对顶角,
∴∠BFE=35°.
∵∠1=65°,
∴∠BEF=115°.由∠BEF+∠B+∠BFE=180°,可得∠B=30°,故B选项正确;
∵∠3=35°,
∴∠EFC=145°.易得∠C=30°,
∴∠C+∠2=30°+65°=95°,
∴∠EFC≠∠C+∠2,故C 选项错误;在△CGF中,∠CFG=35°,∠C=30°,∠CFG>∠C,
∴CG>FG,故D选项正确.故选C;
∵∠3和∠BFE互为对顶角,
∴∠BFE=35°.
∵∠1=65°,
∴∠BEF=115°.由∠BEF+∠B+∠BFE=180°,可得∠B=30°,故B选项正确;
∵∠3=35°,
∴∠EFC=145°.易得∠C=30°,
∴∠C+∠2=30°+65°=95°,
∴∠EFC≠∠C+∠2,故C 选项错误;在△CGF中,∠CFG=35°,∠C=30°,∠CFG>∠C,
∴CG>FG,故D选项正确.故选C;
3. 如图,已知$AB// CD$,$\angle 1:\angle 2:\angle 3= 1:2:3$.求证:$BA平分\angle EBF$.下面给出证法 1.
证法 1:设$\angle 1$,$\angle 2$,$\angle 3的度数分别为x$,$2x$,$3x$.
$\because AB// CD$,$\therefore 2x+3x= 180^{\circ}$,解得$x= 36^{\circ}$.
$\therefore \angle 1= 36^{\circ}$,$\angle 2= 72^{\circ}$,$\angle 3= 108^{\circ}$.
$\because \angle EBD= 180^{\circ}$,$\angle ABD= \angle 1+\angle 2= 108^{\circ}$,
$\therefore \angle EBA= 180^{\circ}-\angle ABD= 72^{\circ}$.
$\therefore \angle EBA= \angle 2$.$\therefore BA平分\angle EBF$.
请阅读证法 1 后,找出与证法 1 不同的证法 2,并写出证明过程.
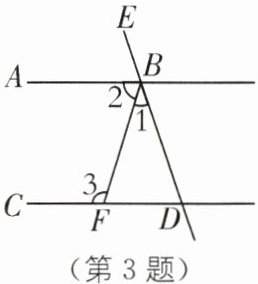
证法 1:设$\angle 1$,$\angle 2$,$\angle 3的度数分别为x$,$2x$,$3x$.
$\because AB// CD$,$\therefore 2x+3x= 180^{\circ}$,解得$x= 36^{\circ}$.
$\therefore \angle 1= 36^{\circ}$,$\angle 2= 72^{\circ}$,$\angle 3= 108^{\circ}$.
$\because \angle EBD= 180^{\circ}$,$\angle ABD= \angle 1+\angle 2= 108^{\circ}$,
$\therefore \angle EBA= 180^{\circ}-\angle ABD= 72^{\circ}$.
$\therefore \angle EBA= \angle 2$.$\therefore BA平分\angle EBF$.
请阅读证法 1 后,找出与证法 1 不同的证法 2,并写出证明过程.

答案:
设∠1,∠2,∠3的度数分别为x,2x,3x,
则∠EBA=180°−3x.
∵AB//CD,
∴∠2=180°−∠3=180°−3x.
∴∠EBA=∠2,即BA平分∠EBF.
则∠EBA=180°−3x.
∵AB//CD,
∴∠2=180°−∠3=180°−3x.
∴∠EBA=∠2,即BA平分∠EBF.
4. (2025·福建泉州石狮期末)如图,已知$\angle ACB= 90^{\circ}$,$CD\perp AB$,垂足为$D$,则下列说法错误的是(

A.$\angle A与\angle B$互为余角
B.$\angle 1与\angle 2$互为余角
C.$\angle 1与\angle A$互为余角
D.$\angle 2与\angle A$互为余角
D
).
A.$\angle A与\angle B$互为余角
B.$\angle 1与\angle 2$互为余角
C.$\angle 1与\angle A$互为余角
D.$\angle 2与\angle A$互为余角
答案:
D [解析]
∵∠ACB=90°,
∴∠A+∠B=90°,∠1+∠2=90°,
∴∠A与∠B互余,∠1与∠2互余,故A,B正确,不符合题意;
∵CD⊥AB,
∴∠A+∠1=90°,∠B+∠2=90°,
∴∠A与∠1互余,∠B与∠2互余,故C正确,不符合题意;D不正确,符合题意,故选D.
∵∠ACB=90°,
∴∠A+∠B=90°,∠1+∠2=90°,
∴∠A与∠B互余,∠1与∠2互余,故A,B正确,不符合题意;
∵CD⊥AB,
∴∠A+∠1=90°,∠B+∠2=90°,
∴∠A与∠1互余,∠B与∠2互余,故C正确,不符合题意;D不正确,符合题意,故选D.
5. (2025·海南三亚期末)已知$AB// CD$,现将一个含有$30^{\circ}角的直角三角尺EFG$按如图方式放置,其中顶点$F$,$G分别落在直线AB$,$CD$上,$GE交AB于点H$,若$\angle EHB= 45^{\circ}$,则$\angle AFG$的度数为(
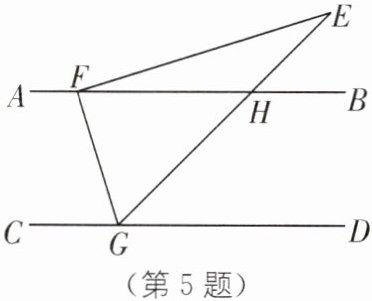
A.$120^{\circ}$
B.$115^{\circ}$
C.$110^{\circ}$
D.$105^{\circ}$
D
).
A.$120^{\circ}$
B.$115^{\circ}$
C.$110^{\circ}$
D.$105^{\circ}$
答案:
D. [解析]
∵AB//CD,
∴∠EGD=∠EHB=45°.
∵∠E=30°,∠FGE=60°,
∴∠FGD=∠FGE+∠EGD=60°+45°=105°.
∴∠AFG=∠FGD=105°.故选D.
∵AB//CD,
∴∠EGD=∠EHB=45°.
∵∠E=30°,∠FGE=60°,
∴∠FGD=∠FGE+∠EGD=60°+45°=105°.
∴∠AFG=∠FGD=105°.故选D.
6. 下列结论推理合理的是(
A.小强和小明体重看起来不等,那么它们一定不等
B.因为王老师是数学老师,所以王老师出的数学题一定没有问题
C.因为小强的妈妈是老师,所以小强学习成绩一定很好
D.因为小强热情、开朗、爱交际,所以小强的朋友可能很多
D
).A.小强和小明体重看起来不等,那么它们一定不等
B.因为王老师是数学老师,所以王老师出的数学题一定没有问题
C.因为小强的妈妈是老师,所以小强学习成绩一定很好
D.因为小强热情、开朗、爱交际,所以小强的朋友可能很多
答案:
D [解析]A.小强和小明体重看起来不等,可能是由于人的视觉误差导致的,它们不一定不等,故A的推理不合理;
B.王老师是数学老师,王老师出的数学题跟他的知识水平有很大的关系,故王老师出的数学题不一定没问题,故B 的推理不合理;C.小强的学习成绩和妈妈是老师没有必然联系,不能武断地说他的学习成绩一定很好,故C的推理不合理;D.小强的朋友多与小强热情、开朗、爱交际有一定联系,故D的推理合理.故选D.
B.王老师是数学老师,王老师出的数学题跟他的知识水平有很大的关系,故王老师出的数学题不一定没问题,故B 的推理不合理;C.小强的学习成绩和妈妈是老师没有必然联系,不能武断地说他的学习成绩一定很好,故C的推理不合理;D.小强的朋友多与小强热情、开朗、爱交际有一定联系,故D的推理合理.故选D.
7. (2025·江苏苏州相城区期末)如图,直线$l_{1}// l_{2}$,将直角三角板按如图方式放置,直角顶点在$l_{2}$上,若$\angle 1= 40^{\circ}$,则$\angle 2= $______.
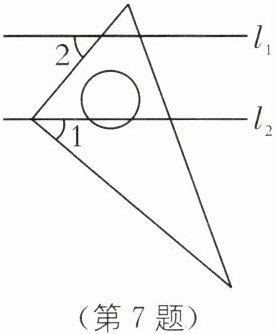

答案:
50° [解析]如图,
∵∠1=40°,
∴∠3=90°−40°=50°.
∵l₁//l₂,
∴∠2=∠3=50°.

50° [解析]如图,
∵∠1=40°,
∴∠3=90°−40°=50°.
∵l₁//l₂,
∴∠2=∠3=50°.

查看更多完整答案,请扫码查看


