第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1.(2025·宁波期末)下列图形中,是轴对称图形的是(
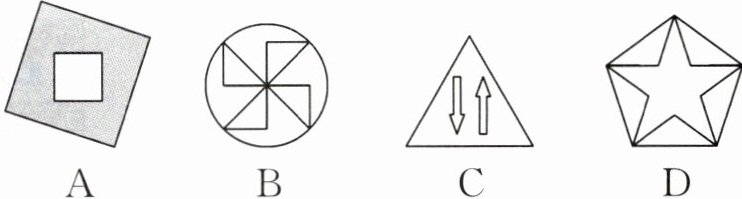
A
B
C D
D
).
A
B
C D
答案:
D
2. 传统文化 甲骨文 (2025·金华永康期末)甲骨文是刻写在龟甲和兽骨上的文字,为我们提供了了解商代历史的珍贵资料.下面是四个甲骨文字,其中是轴对称图形的是(
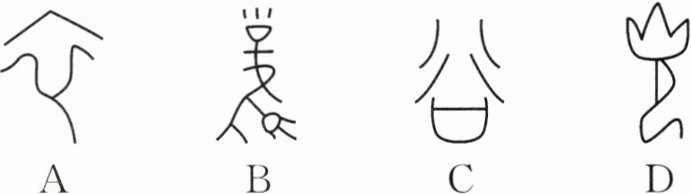
A
B
C D
C
).
A
B
C D
答案:
C
3.(2025·重庆合川区期末)如图,在△ABC中,AB= AC,AB的垂直平分线DE交AB于点D,交AC于点E,若∠CBE= 15°,则∠A的度数为(
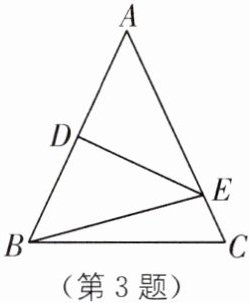
A.45°
B.50°
C.65°
D.70°
B
).
A.45°
B.50°
C.65°
D.70°
答案:
B [解析]由题意得,AE=BE,
∴∠A=∠ABE.
∵AB= AC,
∴∠ABC=∠C.设∠A=∠ABE=x,
∴∠C=∠ABC=∠ABE+∠CBE=x+15°.由条件可知x+2(x+15°)=180°,解得x=50°,
∴∠A的度数为50°.故选B.
∴∠A=∠ABE.
∵AB= AC,
∴∠ABC=∠C.设∠A=∠ABE=x,
∴∠C=∠ABC=∠ABE+∠CBE=x+15°.由条件可知x+2(x+15°)=180°,解得x=50°,
∴∠A的度数为50°.故选B.
4. 如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G,连结AE,AG.
(1)若△AEG的周长为10,求线段BC的长;
(2)若∠BAC= 104°,求∠EAG的度数.
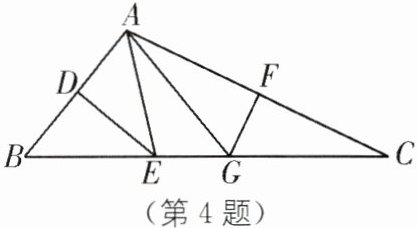
(1)若△AEG的周长为10,求线段BC的长;
(2)若∠BAC= 104°,求∠EAG的度数.

答案:
(1)
∵DE垂直平分AB,GF垂直平分AC,
∴AE=EB,AG=GC.
∵△AEG的周长为10,即AE+EG+AG=10,
∴BC=EB+EG+GC=AE+EG+AG=10.
(2)
∵∠BAC=104°,
∴∠B+∠C=180°-104°=76°.
∵AE=EB,AG=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=76°,
∴∠EAG=∠BAC-(∠EAB+∠GAC)=104°-76°=28°.
归纳总结 本题考查的是线段的垂直平分线的性质、三角形内角和定理,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
(1)
∵DE垂直平分AB,GF垂直平分AC,
∴AE=EB,AG=GC.
∵△AEG的周长为10,即AE+EG+AG=10,
∴BC=EB+EG+GC=AE+EG+AG=10.
(2)
∵∠BAC=104°,
∴∠B+∠C=180°-104°=76°.
∵AE=EB,AG=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=76°,
∴∠EAG=∠BAC-(∠EAB+∠GAC)=104°-76°=28°.
归纳总结 本题考查的是线段的垂直平分线的性质、三角形内角和定理,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
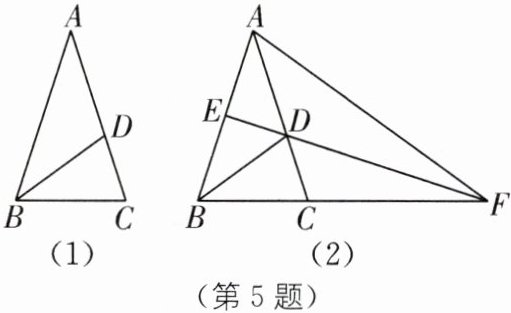
5. 方程思想 (2025·重庆黔江区期末)在△ABC中,AB= AC,BD平分∠ABC,交AC于点D,BD= AD.
(1)如图(1),求∠BAC的度数;
(2)如图(2),E是AB的中点,连结ED并延长,交BC的延长线于点F,连结AF.求证:AF= AB+BC.
(1)如图(1),求∠BAC的度数;
(2)如图(2),E是AB的中点,连结ED并延长,交BC的延长线于点F,连结AF.求证:AF= AB+BC.

答案:
(1)设∠ABD=x°.
∵BD平分∠ABC,
∴∠DBC=x°.
∵AB=AC,
∴∠C=∠ABC=2x°.又BD=AD,
∴∠A=x°.在△ABC中,∠A+∠ABC+∠C=180°,
∴x+2x+2x=180,解得x=36,
∴∠A=36°,
∴∠BAC的度数为36°.
(2)
∵E是AB的中点,BD=AD,
∴EF是AB的垂直平分线,
∴AF=BF,
∴∠FBA=∠FAB=72°,
∴∠AFB=∠FAC=36°,
∴CA=CF,
∴AB=AC=CF,
∴AF=BF=BC+CF=AB+BC.
归纳总结 本题主要考查等腰三角形的性质,掌握线段垂直平分线的性质、等边对等角是解题的关键,注意三角形内角和定理和方程思想的应用.
(1)设∠ABD=x°.
∵BD平分∠ABC,
∴∠DBC=x°.
∵AB=AC,
∴∠C=∠ABC=2x°.又BD=AD,
∴∠A=x°.在△ABC中,∠A+∠ABC+∠C=180°,
∴x+2x+2x=180,解得x=36,
∴∠A=36°,
∴∠BAC的度数为36°.
(2)
∵E是AB的中点,BD=AD,
∴EF是AB的垂直平分线,
∴AF=BF,
∴∠FBA=∠FAB=72°,
∴∠AFB=∠FAC=36°,
∴CA=CF,
∴AB=AC=CF,
∴AF=BF=BC+CF=AB+BC.
归纳总结 本题主要考查等腰三角形的性质,掌握线段垂直平分线的性质、等边对等角是解题的关键,注意三角形内角和定理和方程思想的应用.
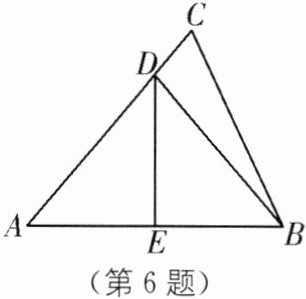
6. 如图,在△ABC中,AB= AC,AB的垂直平分线DE分别交AC,AB于点D,E,连结BD.
(1)若∠A= 50°,求∠CBD的度数;
(2)若AB= 7,△CBD周长为12,求BC的长.
(1)若∠A= 50°,求∠CBD的度数;
(2)若AB= 7,△CBD周长为12,求BC的长.

答案:
(1)
∵AB=AC,∠A=50°,
∴∠ABC=∠C=65°.
∵DE垂直平分AB,
∴DA=DB,
∴∠ABD=∠A=50°,
∴∠CBD=∠ABC-∠ABD=65°-50°=15°.
(2)
∵DE垂直平分AB,
∴DA=DB,
∴DB+DC=DA+DC=AC.又AB=AC=7,△CBD周长为12,
∴BC=5.
(1)
∵AB=AC,∠A=50°,
∴∠ABC=∠C=65°.
∵DE垂直平分AB,
∴DA=DB,
∴∠ABD=∠A=50°,
∴∠CBD=∠ABC-∠ABD=65°-50°=15°.
(2)
∵DE垂直平分AB,
∴DA=DB,
∴DB+DC=DA+DC=AC.又AB=AC=7,△CBD周长为12,
∴BC=5.
查看更多完整答案,请扫码查看


