《2025年实验班提优训练八年级数学上册浙教版》

1. 实验班原创 在平面直角坐标系中,点P(-2025,2024)到y轴的距离是(A).
A.2025
B.-2025
C.2024
D.-2024

答案： A　[解析]在平面直角坐标系中,点P(−2025,2024)到y轴的距离是|−2025|=2025.故选A

2. (2024·嘉兴桐乡期末)已知点P(x,y)在第四象限,且|x|= 3,|y|= 5,则点P的坐标是(C).
A.(-3,-5)
B.(5,-3)
C.(3,-5)
D.(-3,5)

答案： C　[解析]
∵点P(x,y)在第四象限,
∴x＞0,y＜0.又|x|=3,|y|=5,
∴x=3,y=−5,
∴点P的坐标为(3,−5),故选C;

3. (2024·金华东阳期末)如果点A(a,a+2)在x轴上,那么点B(a+3,a-1)的坐标为(A).
A.(1,-3)
B.(2,4)
C.(4,2)
D.(3,-1)

答案： A　[解析]
∵点A(a,a+2)在x轴上,
∴a+2=0,
∴a=−2,
∴点B(1,−3).故选A

4. (2025·北京城区期中)已知点M(-2,1),MN//y轴,若MN= 3,则点N的坐标是(−2,−2)或(−2,4).

答案： (−2,−2)或(−2,4)　[解析]
∵M(−2,1),MN//y轴,
∴点M横坐标与点N横坐标相同.
∵MN=3,
∴点N纵坐标为1+3=4或1−3=−2,即N(−2,4)或(−2,−2).

5. (2025·绍兴诸暨期末)在平面直角坐标系中,第一象限内一点(m,2m-1)到x轴和y轴的距离相等,则m=1.

答案： 1　[解析]
∵第一象限内一点(m,2m−1)到x轴和y轴的距离相等,
∴m=2m−1,
∴m=1.

6. 教材P126例3·变式 如图,AB= DE= GH= MN= 2,其余各短边长均为1,且图中的角都是直角,请建立适当的平面直角坐标系,并写出各个顶点的坐标.

答案：
答案不唯一，建立如图所示的平面直角坐标系，
　　　　　　　
　则A(−2,3),B(−2,1),C(−1,1),D(−1,0),E(1,0),F(1,1),G(2,1),H(2,3),I(1,3),M(1,4),N(−1,4),K(−1,3).

7. 在平面直角坐标系中,一个动点按如图所示的方向移动,即(0,0)→(0,1)→(1,1)→(2,2)→(2,3)→(3,3)→(4,4)→…,以此规律,记(0,0)为第1个点,则第15个点的坐标为(A).

A.(9,9)
B.(8,9)
C.(9,10)
D.(10,10)

答案： A　[解析]
∵(0,0)→(0,1)→(1,1)→(2,2)→(2,3)→(3,3)→(4,4)→…,
∴观察发现,每三个点为一组，第n组最后一个点的坐标为(2n−1,2n−1).
∵15÷3=5,
∴第15个点的坐标为第五组最后一个点的坐标,
∴第15个点的坐标为(9,9).故选A

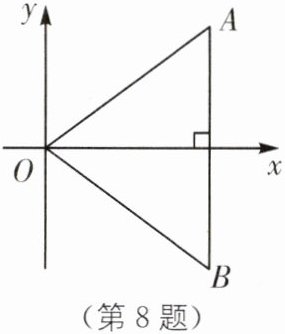
8. 如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB= 6,OA= OB= 5,则点A的坐标是(D).

A.(5,4)
B.(3,4)
C.(5,3)
D.(4,3)

答案： D　[解析]设AB与x轴交于点C.
∵OA=OB,OC⊥AB,AB=6,
∴AC=$\frac{1}{2}$AB=3.
　由勾股定理,得OC=$\sqrt{OA^{2}-AC^{2}}=\sqrt{5^{2}-3^{2}}=4$,
∴点A的坐标为(4,3).故选D.

9. 小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系. 若坐标轴的单位长度取1 mm,则图中转折点P的坐标表示正确的是( ).


A.(5,30)
B.(8,10)
C.(9,10)
D.(10,10)

答案：
C　[解析]如图，过点C作CD⊥y轴于点D,
∴AP=CD=50÷2−16=9(mm),OA=OD−AD=40−30=10(mm),
　　　　　　　　　　　　　　　　
∴P(9,10).故选C.

10. (2024·宁波期中)如图,在平面直角坐标系中,长方形ABCD的四条边与两条坐标轴平行,已知点A(-1,2),点C(1,-1). 点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个单位长度；点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个单位长度. 记P,Q在长方形边上第一次相遇时的点为$M_1,$第二次相遇时的点为$M_2,…,$则$M_2₀_2_4$的坐标为是(D).
A.(1,0)
B.(-1,0)
C.(1,2)
D.(0,-1)

答案： D　[解析]长方形ABCD的周长为(3+2)×2=10,
　设经过t秒P,Q第一次相遇,则点P走的路程为2t,点Q走的路程为3t.
　根据题意,得2t+3t=10,解得t=2,
∴当t=2时,P,Q第一次相遇,此时相遇点M₁坐标为(1,0);
　当t=4时,P,Q第二次相遇,此时相遇点M₂坐标为(−1,0);
　当t=6时,P,Q第三次相遇，此时相遇点M₃坐标为(1,2);
　当t=8时,P,Q第四次相遇,此时相遇点M₄坐标为(0,−1);
　当t=10时,P,Q第五次相遇,此时相遇点M₅坐标为(−1,2);
　当t=12时,P,Q第六次相遇,此时相遇点M₆坐标为(1,0),...
∴五次相遇一循环.
∵2024÷5=404……4,
∴M₂₀₂₄₌的坐标为(0,−1).
　故选D.