第106页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 分类讨论思想 已知 A(-3,0),C(0,4),点 B 在 x 轴上,且 AB= 4.
(1)求点 B 的坐标,在平面直角坐标系中画出 △ABC,并求出△ABC 的面积.
(2)点 P 在 y 轴上,若以 A,C,P 三点为顶点的三角形的面积为 9,求出点 P 的坐标.
(1)求点 B 的坐标,在平面直角坐标系中画出 △ABC,并求出△ABC 的面积.
(2)点 P 在 y 轴上,若以 A,C,P 三点为顶点的三角形的面积为 9,求出点 P 的坐标.
答案:
1.
(1)
∵A(−3,0),C(0,4),点B在x轴上,且AB=4,
∴设点B的坐标为(x,0),|x−(−3)|=4,
解得x=−7或x=1,
∴点B的坐标为(−7,0)或(1,0).
在平面直角坐标系中画出△ABC,如图所示,

∴S△AB₁C=$\frac{[(-3)-(-7)]×4}{2}$=8,
S△AB₂C=$\frac{[1-(-3)]×4}{2}$=8,故△ABC的面积为8.
(2)设点P的坐标为(0,y),
由题意可知点P可能在点C的上方或下方.
当点P在点C的上方时,S△ACP=$\frac{(y-4)×|-3|}{2}$=9,
解得y=10;
当点P在点C的下方时,S△ACP=$\frac{(4-y)×|-3|}{2}$=9,
解得y=-2.
综上所述,点P的坐标为(0,10)或(0,−2).
易错警示 解答本题较易出现失误的是在求点P的坐标时,没有分点P在点C上方和下方两种情况进行分析,造成漏解.
1.
(1)
∵A(−3,0),C(0,4),点B在x轴上,且AB=4,
∴设点B的坐标为(x,0),|x−(−3)|=4,
解得x=−7或x=1,
∴点B的坐标为(−7,0)或(1,0).
在平面直角坐标系中画出△ABC,如图所示,

∴S△AB₁C=$\frac{[(-3)-(-7)]×4}{2}$=8,
S△AB₂C=$\frac{[1-(-3)]×4}{2}$=8,故△ABC的面积为8.
(2)设点P的坐标为(0,y),
由题意可知点P可能在点C的上方或下方.
当点P在点C的上方时,S△ACP=$\frac{(y-4)×|-3|}{2}$=9,
解得y=10;
当点P在点C的下方时,S△ACP=$\frac{(4-y)×|-3|}{2}$=9,
解得y=-2.
综上所述,点P的坐标为(0,10)或(0,−2).
易错警示 解答本题较易出现失误的是在求点P的坐标时,没有分点P在点C上方和下方两种情况进行分析,造成漏解.
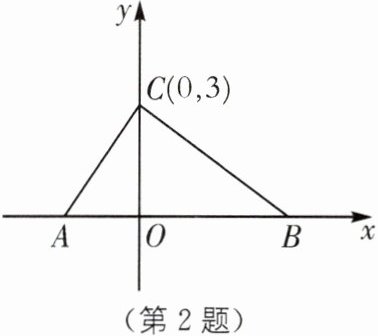
2. 如图,在平面直角坐标系中,点 A,B 的坐标分别为 A(a,0),B(b,0),且 a,b 满足|a+2|$+(b-4)^2= 0,$点 C 的坐标为(0,3).
(1)求 a,b 的值及 S△ABC;
(2)若点 M 在 x 轴上,且 S△ACM= 1/3 S△ABC,试求点 M 的坐标.
(1)求 a,b 的值及 S△ABC;
(2)若点 M 在 x 轴上,且 S△ACM= 1/3 S△ABC,试求点 M 的坐标.

答案:
2.
(1)由题意,得|a+2|=0,(b−4)²=0,
→绝对值,平方的非负性
∴a=−2,b=4,
∴A(−2,0),B(4,0).
又C(0,3),
∴AB=|−2−4|=6,CO=3,
∴S△ABC=$\frac{1}{2}$AB·CO=$\frac{1}{2}$×6×3=9.
(2)设点M的坐标为(x,0),
则AM=|x−(−2)|=|x+2|.
又S△ACM=$\frac{1}{3}$S△ABC,
∴$\frac{1}{2}$AM·OC=$\frac{1}{3}$×9=3,
∴|x+2|×3=6,
∴|x+2|=2,解得x=0或-4.故点M的坐标为(0,0)或(−4,0).
知识拓展 如图
(1),当点A,B在x轴上时,则S△ABC=$\frac{1}{2}$AB·CD=$\frac{1}{2}$|x_B-x_A|·|y_C|;如图
(2),当点A,B在y轴上时,则S△ABC=$\frac{1}{2}$AB·CD=$\frac{1}{2}$|y_A-y_B|·|x_C|.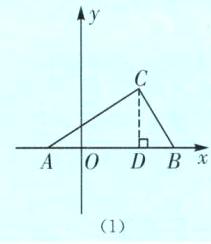

2.
(1)由题意,得|a+2|=0,(b−4)²=0,
→绝对值,平方的非负性
∴a=−2,b=4,
∴A(−2,0),B(4,0).
又C(0,3),
∴AB=|−2−4|=6,CO=3,
∴S△ABC=$\frac{1}{2}$AB·CO=$\frac{1}{2}$×6×3=9.
(2)设点M的坐标为(x,0),
则AM=|x−(−2)|=|x+2|.
又S△ACM=$\frac{1}{3}$S△ABC,
∴$\frac{1}{2}$AM·OC=$\frac{1}{3}$×9=3,
∴|x+2|×3=6,
∴|x+2|=2,解得x=0或-4.故点M的坐标为(0,0)或(−4,0).
知识拓展 如图
(1),当点A,B在x轴上时,则S△ABC=$\frac{1}{2}$AB·CD=$\frac{1}{2}$|x_B-x_A|·|y_C|;如图
(2),当点A,B在y轴上时,则S△ABC=$\frac{1}{2}$AB·CD=$\frac{1}{2}$|y_A-y_B|·|x_C|.


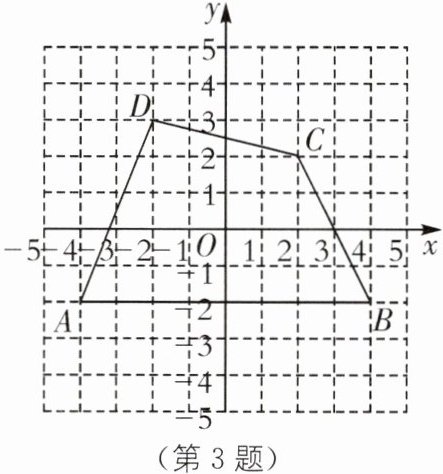
3. 割补法 如图,在平面直角坐标系中,四边形 ABCD 的各个顶点的坐标分别为 A(-4,-2),B(4,-2),C(2,2),D(-2,3).求四边形 ABCD 的面积.

答案:
3.如图,过点D作DF⊥AB交AB于点F,过点C分别作CE⊥AB交AB于点E,作CG⊥DF交DF于点G, S四边形ABCD=S△ADF+S△CDG+S△BCE+S正方形EFG C=$\frac{1}{2}$×2×5+$\frac{1}{2}$×1×4+$\frac{1}{2}$×2×4+4×4=5+2+4+16=27.
S四边形ABCD=S△ADF+S△CDG+S△BCE+S正方形EFG C=$\frac{1}{2}$×2×5+$\frac{1}{2}$×1×4+$\frac{1}{2}$×2×4+4×4=5+2+4+16=27.
3.如图,过点D作DF⊥AB交AB于点F,过点C分别作CE⊥AB交AB于点E,作CG⊥DF交DF于点G,
 S四边形ABCD=S△ADF+S△CDG+S△BCE+S正方形EFG C=$\frac{1}{2}$×2×5+$\frac{1}{2}$×1×4+$\frac{1}{2}$×2×4+4×4=5+2+4+16=27.
S四边形ABCD=S△ADF+S△CDG+S△BCE+S正方形EFG C=$\frac{1}{2}$×2×5+$\frac{1}{2}$×1×4+$\frac{1}{2}$×2×4+4×4=5+2+4+16=27. 4. 实验班原创 已知点 A(a,4),B(-1,b),C(2,-2),AB//x 轴,AC//y 轴.
(1)求 a,b 的值.
(2)求△ABC 的面积.
(3)直线 AB 上是否存在一点 D,使 S△ACD= 1/3 S△ABC?若存在,求出点 D 的坐标;反之,请说明理由.
(1)求 a,b 的值.
(2)求△ABC 的面积.
(3)直线 AB 上是否存在一点 D,使 S△ACD= 1/3 S△ABC?若存在,求出点 D 的坐标;反之,请说明理由.
答案:
4.
(1)因为AB//x轴,AC//y轴,所以a=2,b=4.
(2)S△ABC=$\frac{1}{2}$×3×6=9.
(3)存在这样的点D.由题意可知,AB=3AD,则点D的坐标为(1,4)或(3,4).
知识拓展 如图
(1),当AB//x轴时,则S△ABC=$\frac{1}{2}$AB·CD=$\frac{1}{2}$|x_B-x_A|·|y_C-y_D|;如图
(2),当AB//y轴时,则S△ABC=$\frac{1}{2}$AB·CD=$\frac{1}{2}$|y_A-y_B|·|x_C-x_D|.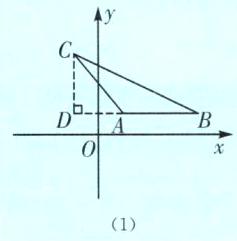

4.
(1)因为AB//x轴,AC//y轴,所以a=2,b=4.
(2)S△ABC=$\frac{1}{2}$×3×6=9.
(3)存在这样的点D.由题意可知,AB=3AD,则点D的坐标为(1,4)或(3,4).
知识拓展 如图
(1),当AB//x轴时,则S△ABC=$\frac{1}{2}$AB·CD=$\frac{1}{2}$|x_B-x_A|·|y_C-y_D|;如图
(2),当AB//y轴时,则S△ABC=$\frac{1}{2}$AB·CD=$\frac{1}{2}$|y_A-y_B|·|x_C-x_D|.


查看更多完整答案,请扫码查看


