第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
6. 中考新考法 操作探究 (2024·山东聊城茌平区期末)如图,已知 BD 是△ABC 的角平分线,CD 是△ABC 的外角∠ACE 的平分线,CD 与 BD 交于点 D.
(1)若∠A= 50°,则∠D= ______
(2)若∠A= 80°,则∠D= ______
(3)若∠A= 130°,则∠D= ______
(4)若∠D= 36°,则∠A= ______
(5)综上所述,你会得到什么结论?证明你的结论的准确性.
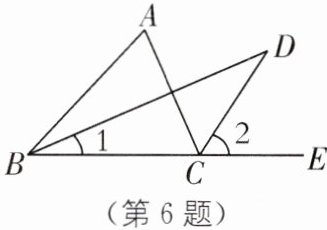
(1)若∠A= 50°,则∠D= ______
25°
.(2)若∠A= 80°,则∠D= ______
40°
.(3)若∠A= 130°,则∠D= ______
65°
.(4)若∠D= 36°,则∠A= ______
72°
.(5)综上所述,你会得到什么结论?证明你的结论的准确性.

结论:∠D= $\frac{1}{2}$∠A. 证明如下:
如题图,
∵BD 是△ABC 的角平分线,CD 是△ABC 的外角∠ACE 的平分线,
∴∠ACE=2∠2,∠ABC=2∠1,
由题可知∠ACE=180°-∠ACB=180°-(180°-∠ABC-∠A)=∠ABC+∠A,
∴2∠2=2∠1+∠A,
而∠2=180°-∠BCD=180°-(180°-∠1-∠D)=∠1+∠D,
∴2∠2=2∠1+2∠D,
∴∠A=2∠D,即∠D= $\frac{1}{2}$∠A.
如题图,
∵BD 是△ABC 的角平分线,CD 是△ABC 的外角∠ACE 的平分线,
∴∠ACE=2∠2,∠ABC=2∠1,
由题可知∠ACE=180°-∠ACB=180°-(180°-∠ABC-∠A)=∠ABC+∠A,
∴2∠2=2∠1+∠A,
而∠2=180°-∠BCD=180°-(180°-∠1-∠D)=∠1+∠D,
∴2∠2=2∠1+2∠D,
∴∠A=2∠D,即∠D= $\frac{1}{2}$∠A.
答案:
(1)25°
(2)40°
(3)65°
(4)72°
(5)结论:∠D= $\frac{1}{2}$∠A. 证明如下:
如题图,
∵BD 是△ABC 的角平分线,CD 是△ABC 的外角∠ACE 的平分线,
∴∠ACE=2∠2,∠ABC=2∠1,
由题可知∠ACE=180°-∠ACB=180°-(180°-∠ABC-∠A)=∠ABC+∠A,
∴2∠2=2∠1+∠A,
而∠2=180°-∠BCD=180°-(180°-∠1-∠D)=∠1+∠D,
∴2∠2=2∠1+2∠D,
∴∠A=2∠D,即∠D= $\frac{1}{2}$∠A.
(1)25°
(2)40°
(3)65°
(4)72°
(5)结论:∠D= $\frac{1}{2}$∠A. 证明如下:
如题图,
∵BD 是△ABC 的角平分线,CD 是△ABC 的外角∠ACE 的平分线,
∴∠ACE=2∠2,∠ABC=2∠1,
由题可知∠ACE=180°-∠ACB=180°-(180°-∠ABC-∠A)=∠ABC+∠A,
∴2∠2=2∠1+∠A,
而∠2=180°-∠BCD=180°-(180°-∠1-∠D)=∠1+∠D,
∴2∠2=2∠1+2∠D,
∴∠A=2∠D,即∠D= $\frac{1}{2}$∠A.
7. (2025·江苏南通海门区期中)如图,把△ABC 沿线段 DE 折叠,使点 A 落在点 F 处,BC//DE;若∠B= 50°,则∠BDF 的度数为(
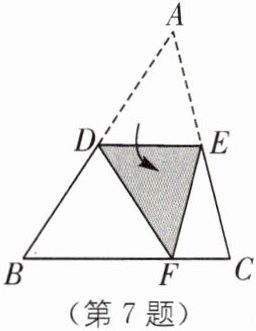
A.40°
B.50°
C.80°
D.100°
C
).
A.40°
B.50°
C.80°
D.100°
答案:
C [解析]
∵BC//DE,∠B=50°,
∴∠ADE=50°,∠DFB=∠EDF.
又△ABC 沿线段 DE 折叠,使点 A 落在点 F 处,
∴∠EDF=∠ADE=∠DFB=50°,
∴∠BDF=180°-50°-50°=80°. 故选 C.
∵BC//DE,∠B=50°,
∴∠ADE=50°,∠DFB=∠EDF.
又△ABC 沿线段 DE 折叠,使点 A 落在点 F 处,
∴∠EDF=∠ADE=∠DFB=50°,
∴∠BDF=180°-50°-50°=80°. 故选 C.
8. (2025·广东东莞期中)如图,M,N 分别是△ABC 的边 AB,AC 上一点,将△ABC 沿 MN 折叠,使点 A 落在边 BC 上,若∠1+∠2+∠3+∠4= 235°,则∠A 的度数为(
A.35°
B.45°
C.65°
D.55°
D
).A.35°
B.45°
C.65°
D.55°
答案:
D [解析]
∵∠1+∠2+∠3+∠4=235°,∠1+∠4+∠B=180°,∠2+∠3+∠C=180°,
∴∠C+∠B=360°-(∠1+∠2+∠3+∠4)=125°.
∵∠A+∠C+∠B=180°,
∴∠A=180°-(∠C+∠B)=55°.故选 D.
∵∠1+∠2+∠3+∠4=235°,∠1+∠4+∠B=180°,∠2+∠3+∠C=180°,
∴∠C+∠B=360°-(∠1+∠2+∠3+∠4)=125°.
∵∠A+∠C+∠B=180°,
∴∠A=180°-(∠C+∠B)=55°.故选 D.
9. (2025·河南洛阳期末)在△ABC 中,∠C= 90°,∠B= 34°,点 M,N 分别在 AB,BC 边上,将△BMN 沿 MN 折叠,使点 B 落在直线 AC 上的点 B′处,当△AB′M 为直角三角形时,∠BNM 的度数为______
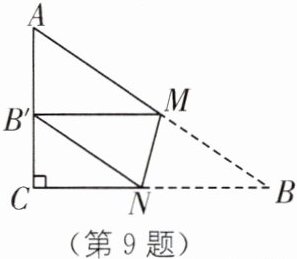
101°或 73°
.
答案:
101°或 73°
10. 风筝模型 如图,把△ABC 沿 EF 折叠,使点 A 落在点 D 处.
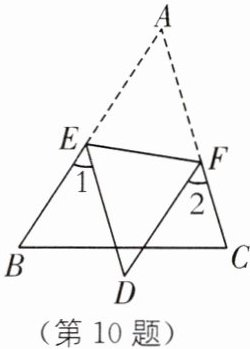
(1)若 DE//AC,试判断∠1 与∠2 的数量关系,并说明理由;
(2)若∠B+∠C= 130°,求∠1+∠2 的度数.

(1)若 DE//AC,试判断∠1 与∠2 的数量关系,并说明理由;
(2)若∠B+∠C= 130°,求∠1+∠2 的度数.
答案:
(1)∠1=∠2,理由如下:
∵∠D 是由∠A 翻折得到,
∴∠D=∠A.
∵DE//AC,
∴∠1=∠A,∠2=∠D,
∴∠1=∠2.
(2)
∵∠A+∠B+∠C=180°,∠B+∠C=130°,
∴∠A=50°,
∴∠AEF+∠AFE=180°-∠A=130°.由折叠知∠AEF=∠DEF,∠AFE=∠DFE.
∴∠1+∠2=(180°-∠AEF-∠DEF)+(180°-∠AFE-∠DFE)=360°-2(∠AEF+∠AFE)=360°-260°=100°.
(1)∠1=∠2,理由如下:
∵∠D 是由∠A 翻折得到,
∴∠D=∠A.
∵DE//AC,
∴∠1=∠A,∠2=∠D,
∴∠1=∠2.
(2)
∵∠A+∠B+∠C=180°,∠B+∠C=130°,
∴∠A=50°,
∴∠AEF+∠AFE=180°-∠A=130°.由折叠知∠AEF=∠DEF,∠AFE=∠DFE.
∴∠1+∠2=(180°-∠AEF-∠DEF)+(180°-∠AFE-∠DFE)=360°-2(∠AEF+∠AFE)=360°-260°=100°.
11. (2024·江西南昌期末改编)已知△ABC 中,∠A= 65°,将∠B,∠C 按照如图所示折叠,若∠ADB′= 35°,求∠1+∠2+∠3 的度数.
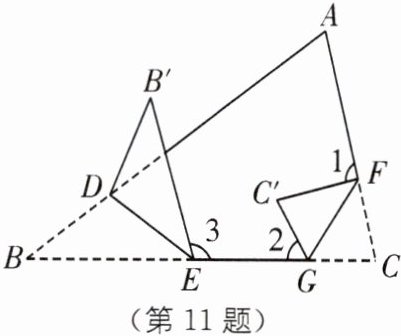

答案:
如图,由折叠知,∠B=∠B',∠C=∠C'.
∵∠3=180°-∠BEB'=180°-(180°-∠B'-∠4)=∠B'+∠4,∠4=180°-∠DMB'=180°-(180°-∠ADB'-∠B')=∠ADB'+∠B',
∴∠3=∠B'+∠ADB'+∠B'=2∠B+35°.
∵∠1+∠2=180°-∠C'GC+180°-∠C'FC=360°-(∠C'FC+∠C'GC),
∠C'FC+∠C'GC=360°-∠C-∠C'=360°-2∠C,
∴∠1+∠2=360°-(∠C'FC+∠C'GC)=360°-(360°-2∠C)=2∠C.
∴∠1+∠2+∠3=2∠C+2∠B+35°=2(∠C+∠B)+35°=2(180°-∠A)+35°=2×(180°-65°)+35°=265°.

如图,由折叠知,∠B=∠B',∠C=∠C'.
∵∠3=180°-∠BEB'=180°-(180°-∠B'-∠4)=∠B'+∠4,∠4=180°-∠DMB'=180°-(180°-∠ADB'-∠B')=∠ADB'+∠B',
∴∠3=∠B'+∠ADB'+∠B'=2∠B+35°.
∵∠1+∠2=180°-∠C'GC+180°-∠C'FC=360°-(∠C'FC+∠C'GC),
∠C'FC+∠C'GC=360°-∠C-∠C'=360°-2∠C,
∴∠1+∠2=360°-(∠C'FC+∠C'GC)=360°-(360°-2∠C)=2∠C.
∴∠1+∠2+∠3=2∠C+2∠B+35°=2(∠C+∠B)+35°=2(180°-∠A)+35°=2×(180°-65°)+35°=265°.

查看更多完整答案,请扫码查看


