《2025年实验班提优训练八年级数学上册浙教版》

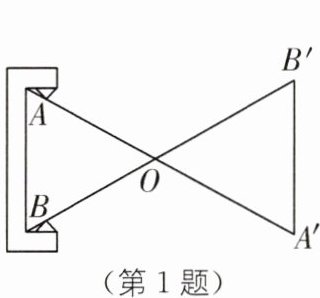
1. (教材 P33 做一做·变式)(2025·河南南阳社旗期中)如图,工人师傅设计了一种测零件内径 AB 的卡钳,卡钳交叉点 O 为 AA',BB'的中点,只要量出 A'B'的长度,就可以知道该零件内径 AB 的长度. 依据的数学基本事实是(B).

A.平行线间的距离处处相等
B.两边和它们的夹角分别相等的两个三角形全等
C.三边分别相等的两个三角形全等
D.两点之间线段最短
]

答案： 【解析】：
本题可根据已知条件判断$\triangle AOB$与$\triangle A'OB'$的关系，再结合全等三角形的性质来确定依据的数学基本事实。
已知卡钳交叉点$O$为$AA'$，$BB'$的中点，则$AO = A'O$，$BO = B'O$。
又因为$\angle AOB$与$\angle A'OB'$是对顶角，根据对顶角的性质可知$\angle AOB=\angle A'OB'$。
在$\triangle AOB$和$\triangle A'OB'$中，$AO = A'O$，$\angle AOB=\angle A'OB'$，$BO = B'O$，满足两边及其夹角分别相等的条件。
根据全等三角形的判定定理“两边和它们的夹角分别相等的两个三角形全等”（$SAS$），可以得出$\triangle AOB\cong\triangle A'OB'$。
再根据全等三角形的性质“全等三角形的对应边相等”，因为$AB$与$A'B'$是对应边，所以$AB = A'B'$，即只要量出$A'B'$的长度，就可以知道该零件内径$AB$的长度。
所以依据的数学基本事实是两边和它们的夹角分别相等的两个三角形全等。
【答案】：B

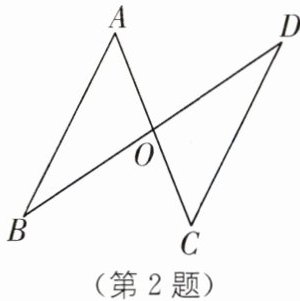
2. (2025·福建泉州永春一中期中)如图,已知 AO= CO,若以“SAS”为依据证明△AOB≌△COD,还要添加的条件是______BO=DO.

答案： 【解析】：
本题可根据全等三角形判定定理“SAS”（边角边）来确定还需添加的条件。“SAS”判定定理是指两边及其夹角对应相等的两个三角形全等。
在$\triangle AOB$和$\triangle COD$中，已知$AO = CO$，这是一组对应边相等，同时$\angle AOB$与$\angle COD$是对顶角，根据对顶角的性质可知$\angle AOB=\angle COD$，即已经有一组边和一组角对应相等，那么要使用“SAS”判定定理证明$\triangle AOB\cong\triangle COD$，还需要添加的条件是另一组对应边相等，且这组边是已知相等边$AO$与$CO$的另一组对应边，即$BO = DO$。
【答案】：$BO = DO$

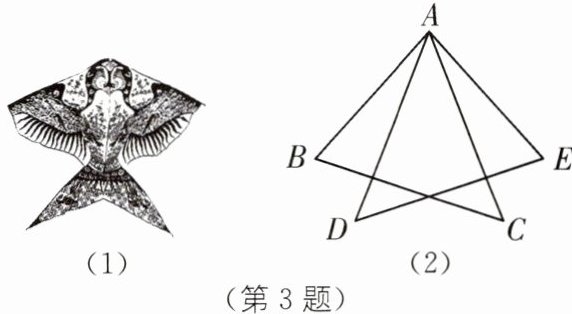
3. 手拉手模型 如图(1)是小军制作的燕子风筝,燕子风筝的骨架图如图(2)所示,AB= AE,AC= AD,∠BAD= ∠EAC,∠C= 50°,求∠D 的大小.

答案： 【解析】：根据题目条件，AB=AE, AC=AD, ∠BAD=∠EAC，可利用SAS（边角边）全等条件判定两个三角形全等，进而利用全等三角形的性质，即对应角相等，来求解∠D的大小。
【答案】：
证明：
∵ $\angle BAD = \angle EAC$，
∴ $\angle BAD + \angle DAC = \angle EAC + \angle DAC$，
即 $\angle BAC = \angle EAD$。
在$\triangle BAC$和$\triangle EAD$中，
$AB = AE$ , $\angle BAC = \angle EAD$ , $AC = AD$，
∴ $\triangle BAC \cong \triangle EAD(SAS)$。
∴ $\angle D = \angle C$ （全等三角形的对应角相等）。
∵ $\angle C = 50^\circ$，
∴ $\angle D = 50^\circ$。

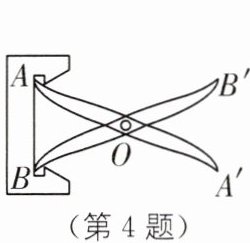
4. (2025·温州期末)如图,把两根钢条 AA',BB'的中点连在一起,可以做成一个测量工件内槽宽的卡钳,若求 AB 的长,只需测量下列线段中的(A).

A.A'B'
B.OA'
C.OB'
D.OA
]

答案： 【解析】：
本题可根据全等三角形的判定定理和性质来求解。
已知$O$是$AA'$，$BB'$的中点，所以$AO = A'O$，$BO = B'O$。
在$\triangle AOB$和$\triangle A'OB'$中，$\begin{cases}AO = A'O\\\angle AOB = \angle A'OB'\\BO = B'O\end{cases}$，根据“边角边”（$SAS$）定理可判定$\triangle AOB\cong\triangle A'OB'$。
根据全等三角形的性质：全等三角形的对应边相等，因为$\triangle AOB\cong\triangle A'OB'$，所以$AB = A'B'$。
那么要求$AB$的长，只需测量$A'B'$的长即可。
【答案】：A。

5. (2024·华东师大附属台州学校期中)如图,AD 是△ABC 的边 BC 上的中线,AB= 7,AD= 5,则 AC 的取值范围为______.

3＜AC＜17

答案： 【解析】：
本题可根据三角形全等的判定和性质，通过延长$AD$构造全等三角形，再利用三角形三边关系来求解$AC$的取值范围。
步骤一：延长$AD$至点$E$，使$DE = AD$，连接$BE$。
因为$AD$是$\triangle ABC$的边$BC$上的中线，所以$BD = CD$。
在$\triangle BDE$和$\triangle CDA$中，$\begin{cases}BD = CD\\\angle BDE = \angle CDA\\DE = DA\end{cases}$，根据“边角边”（$SAS$）判定定理，可得$\triangle BDE\cong\triangle CDA$。
步骤二：根据全等三角形的性质得到$BE = AC$。
步骤三：在$\triangle ABE$中，利用三角形三边关系求出$AE$的取值范围。
已知$AB = 7$，$AD = 5$，则$AE = 2AD = 10$。
根据三角形三边关系“两边之和大于第三边，两边之差小于第三边”，可得$AB - BE\lt AE\lt AB + BE$，即$7 - BE\lt 10\lt 7 + BE$。
解不等式$7 - BE\lt 10$，可得$BE\gt -3$（边长不能为负，此不等式恒成立）；
解不等式$10\lt 7 + BE$，可得$BE\gt 3$。
同时，$BE\lt AB + AE = 7 + 10 = 17$（此为大致范围，还需结合前面推导）。
更准确的由$AE - AB\lt BE\lt AE + AB$，即$10 - 7\lt BE\lt 10 + 7$，所以$3\lt BE\lt 17$。
步骤四：因为$BE = AC$，所以得出$AC$的取值范围。
即$3\lt AC\lt 17$。
【答案】：$3\lt AC\lt 17$

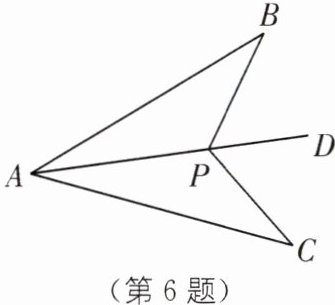
6. 中考新考法 添加条件开放 (2025·湖北武汉黄陂区期末)如图所示,已知 P 是∠BAC 的平分线 AD 上的一点,请添加一个条件：AB=AC,使得△ABP≌△ACP.
]

答案： 【解析】：本题考查三角形全等的判定。
题目给出了两个三角形$\triangle ABP$和$\triangle ACP$，其中$AP$是两个三角形的公共边，且$AD$是$\angle BAC$的平分线，所以$\angle BAP=\angle CAP$。
为了证明$\triangle ABP\cong\triangle ACP$，根据全等三角形的判定定理，有以下几种情况：
$SAS$判定：已知$AP$是公共边，$\angle BAP=\angle CAP$，如果$AB=AC$，则可以根据$SAS$判定$\triangle ABP\cong\triangle ACP$。
$ASA$判定：已知$\angle BAP=\angle CAP$，$AP$是公共边，如果$\angle APB=\angle APC$，则可以根据$ASA$判定$\triangle ABP\cong\triangle ACP$。
$AAS$判定：已知$\angle BAP=\angle CAP$，$AP$是公共边，如果$\angle ABP=\angle ACP$，则可以根据$AAS$判定$\triangle ABP\cong\triangle ACP$。
因此，可以添加的条件有很多，比如$AB=AC$或$\angle APB=\angle APC$或$\angle ABP=\angle ACP$等。
【答案】：$AB=AC$（答案不唯一）。

7. (2024·金华东阳期末)如图,AF= DC,∠BCA= ∠EFD,BC= EF,求证：△ABC≌△DEF.
]

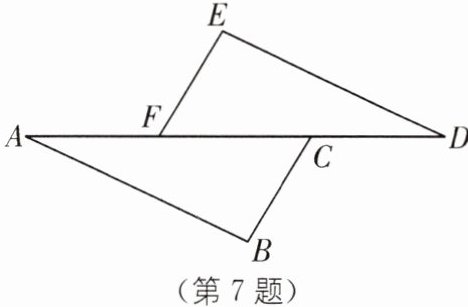
答案： 证明：
∵ AF = DC，
∴ AF + FC = DC + FC，即 AC = DF。
在△ABC 和△DEF 中，
$\left\{\begin{array}{l} AC=DF,\\ ∠BCA=∠EFD,\\ BC=EF,\end{array}\right.$
∴ △ABC≌△DEF（SAS）。