第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
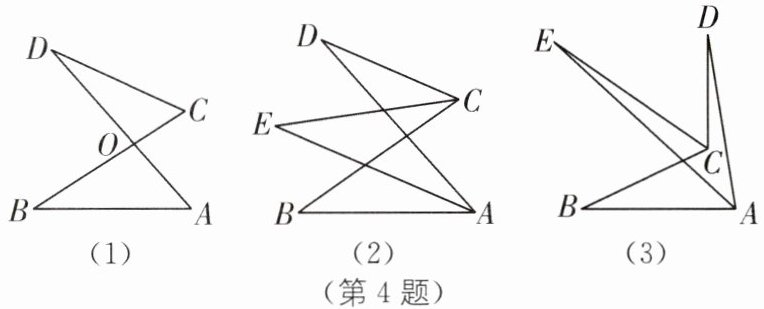
4.(1)[模型]如图(1),AD,BC 交于 O 点.求证:∠D+∠C= ∠A+∠B.
(2)[模型应用]如图(2),∠BAD 和∠BCD 的平分线交于点 E.
①若∠D= 20°,∠B= 60°,则∠E 的度数是 ;
②直接写出∠E 与∠D,∠B 之间的数量关系是 ;
(3)[类比应用]如图(3),∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E.若∠D= m°,∠B= n°(m<n).求∠E 的度数.(用含有 m,n 的式子表示)
(2)[模型应用]如图(2),∠BAD 和∠BCD 的平分线交于点 E.
①若∠D= 20°,∠B= 60°,则∠E 的度数是 ;
②直接写出∠E 与∠D,∠B 之间的数量关系是 ;
(3)[类比应用]如图(3),∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E.若∠D= m°,∠B= n°(m<n).求∠E 的度数.(用含有 m,n 的式子表示)

答案:
4.
(1)
∵∠D+∠C+∠COD=∠A+∠B+∠AOB=180°,∠COD=∠AOB,
∴∠D+∠C=∠A+∠B。
(2)①40° [解析]如题图
(2),
∵∠D+∠DCE=∠E+∠DAE,∠E+∠ECB=∠B+∠EAB,
∴∠D+∠DCE+∠B+∠EAB=2∠E+∠DAE+∠ECB。
∵CE平分∠DCB,AE平分∠BAD,
∴∠DCE=∠ECB,∠DAE=∠BAE,
∴2∠E=∠B+∠D,
∴∠E=$\frac{1}{2}$×(20°+60°)=$\frac{1}{2}$×80°=40°。
②∠E=$\frac{1}{2}$(∠D+∠B) [解析]如题图
(2),∠D+∠DCE=∠E+∠DAE,∠B+∠BAE=∠E+∠ECB,
∴∠D+∠DCE+∠B+∠BAE=2∠E+∠DAE+∠ECB。
∵CE,AE分别是∠BCD,∠BAD的平分线,
∴∠DCE=∠BCE,∠DAE=∠BAE。
∴2∠E=∠D+∠B,
∴∠E=$\frac{1}{2}$(∠D+∠B)。
(3)如图,延长BC交AD于点F,
∵∠BFD=∠B+∠BAD,
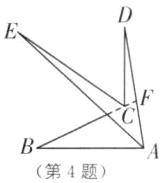
∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D。
∵CE平分∠BCD,AE平分∠BAD,
∴∠ECD=∠ECB=$\frac{1}{2}$∠BCD,∠EAD=∠EAB=$\frac{1}{2}$∠BAD。
∵∠E+∠ECB=∠B+∠EAB,
∴∠E=∠B+∠EAB−∠ECB=∠B+∠BAE−$\frac{1}{2}$∠BCD=∠B+∠BAE−$\frac{1}{2}$(∠B+∠BAD+∠D)=$\frac{1}{2}$(∠B−∠D)。
∵∠D=m°,∠B=n°,
∴∠E=$\frac{1}{2}$(n−m)°。
4.
(1)
∵∠D+∠C+∠COD=∠A+∠B+∠AOB=180°,∠COD=∠AOB,
∴∠D+∠C=∠A+∠B。
(2)①40° [解析]如题图
(2),
∵∠D+∠DCE=∠E+∠DAE,∠E+∠ECB=∠B+∠EAB,
∴∠D+∠DCE+∠B+∠EAB=2∠E+∠DAE+∠ECB。
∵CE平分∠DCB,AE平分∠BAD,
∴∠DCE=∠ECB,∠DAE=∠BAE,
∴2∠E=∠B+∠D,
∴∠E=$\frac{1}{2}$×(20°+60°)=$\frac{1}{2}$×80°=40°。
②∠E=$\frac{1}{2}$(∠D+∠B) [解析]如题图
(2),∠D+∠DCE=∠E+∠DAE,∠B+∠BAE=∠E+∠ECB,
∴∠D+∠DCE+∠B+∠BAE=2∠E+∠DAE+∠ECB。
∵CE,AE分别是∠BCD,∠BAD的平分线,
∴∠DCE=∠BCE,∠DAE=∠BAE。
∴2∠E=∠D+∠B,
∴∠E=$\frac{1}{2}$(∠D+∠B)。
(3)如图,延长BC交AD于点F,
∵∠BFD=∠B+∠BAD,

∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D。
∵CE平分∠BCD,AE平分∠BAD,
∴∠ECD=∠ECB=$\frac{1}{2}$∠BCD,∠EAD=∠EAB=$\frac{1}{2}$∠BAD。
∵∠E+∠ECB=∠B+∠EAB,
∴∠E=∠B+∠EAB−∠ECB=∠B+∠BAE−$\frac{1}{2}$∠BCD=∠B+∠BAE−$\frac{1}{2}$(∠B+∠BAD+∠D)=$\frac{1}{2}$(∠B−∠D)。
∵∠D=m°,∠B=n°,
∴∠E=$\frac{1}{2}$(n−m)°。
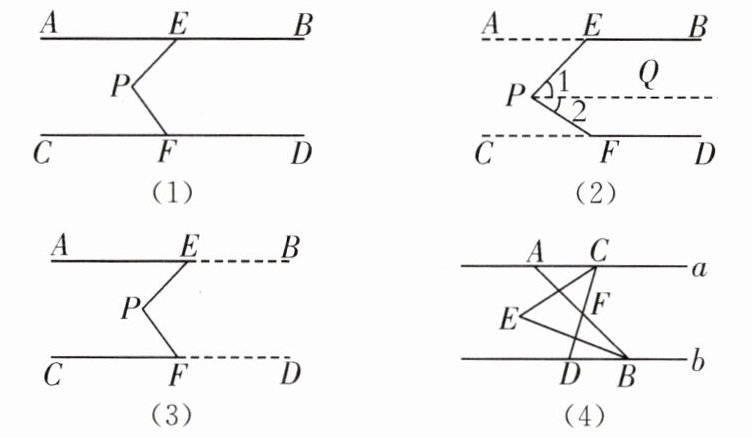
5.[图形感知]如图(1),AB//CD,点 E 在直线 AB 上,点 F 在直线 CD 上,点 P 为 AB,CD 之间一点.
(1)如图(2),该基本图形称为“铅笔头型”(实线部分),它有一个常用数学结论:∠BEP+∠PFD+∠EPF= 360°,它可以通过如下方法证明,请你帮忙完成该结论的推理过程.
证明:如图(2),过点 P 作 PQ//BE.
∵AB//CD,PQ//BE(已知),
∴PQ// (平行于同一条直线的两条直线平行),
∴∠1+∠BEP= 180°,∠2+∠PFD= 180°( ),
∴∠1+∠BEP+∠2+∠PFD= 360°(等式的性质),
∴∠BEP+∠PFD+∠EPF= 360°.
(2)如图(3),该基本图形称为“M 型”(实线部分),仿照上面结论的推理思路可得∠AEP,∠CFP,∠EPF 之间的关系是 ;
[结论应用]直接利用上述结论进行证明;
(3)如图(4),直线 a//b,点 A,C 在直线 a 上,点 B,D 在直线 b 上,直线 CE,BE 分别平分∠ACD,∠ABD,且交于点 E.猜想并证明∠CEB 与∠AFD 的数量关系;
[拓展延伸]
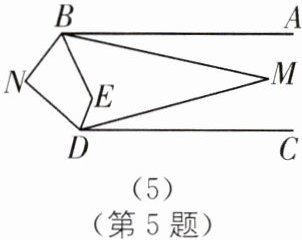
(4)如图(5),已知 AB//CD,∠ABN 与∠CDN 两个角的平分线相交于点 E.若∠ABM= 1/n∠ABE,∠CDM= 1/n∠CDE,设∠M= m°,∠N= °.(用含有 n,m 的代数式表示)
(1)如图(2),该基本图形称为“铅笔头型”(实线部分),它有一个常用数学结论:∠BEP+∠PFD+∠EPF= 360°,它可以通过如下方法证明,请你帮忙完成该结论的推理过程.
证明:如图(2),过点 P 作 PQ//BE.
∵AB//CD,PQ//BE(已知),
∴PQ// (平行于同一条直线的两条直线平行),
∴∠1+∠BEP= 180°,∠2+∠PFD= 180°( ),
∴∠1+∠BEP+∠2+∠PFD= 360°(等式的性质),
∴∠BEP+∠PFD+∠EPF= 360°.
(2)如图(3),该基本图形称为“M 型”(实线部分),仿照上面结论的推理思路可得∠AEP,∠CFP,∠EPF 之间的关系是 ;
[结论应用]直接利用上述结论进行证明;
(3)如图(4),直线 a//b,点 A,C 在直线 a 上,点 B,D 在直线 b 上,直线 CE,BE 分别平分∠ACD,∠ABD,且交于点 E.猜想并证明∠CEB 与∠AFD 的数量关系;
[拓展延伸]
(4)如图(5),已知 AB//CD,∠ABN 与∠CDN 两个角的平分线相交于点 E.若∠ABM= 1/n∠ABE,∠CDM= 1/n∠CDE,设∠M= m°,∠N= °.(用含有 n,m 的代数式表示)


答案:
5.
(1)CD 两直线平行,同旁内角互补
(2)∠EPF=∠AEP+∠CFP [解析]如图,过点P作PM//AB,
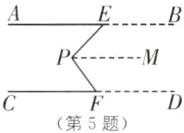
∵AB//CD,
∴AB//CD//PM,
∴∠AEP=∠MPE,∠CFP=∠MPF,
∴∠EPF=∠MPE+∠MPF=∠AEP+∠CFP,
即∠EPF=∠AEP+∠CFP。
(3)∠AFD=2∠CEB,理由如下:
由
(2),得∠CEB=∠ACE+∠DBE,∠AFD=∠CFB=∠ACF+∠DBF。
∵CE平分∠ACD,BE平分∠ABD,
∴∠ACD=2∠ACE,∠DBF=2∠DBE,
∴∠AFD=2∠CEB。
(4)(360 - 2mn) [解析]
∵∠ABN与∠CDN两个角的平分线相交于点E,
∴∠ABE=$\frac{1}{2}$∠ABN,∠CDE=$\frac{1}{2}$∠CDN。
∵∠ABM=$\frac{1}{n}$∠ABE,∠CDM=$\frac{1}{n}$∠CDE,
∴∠ABE=n∠ABM,∠CDE=n∠CDM,
∴∠ABN=2n∠ABM,∠CDN=2n∠CDM。
由
(1),得∠ABN+∠N+∠CDN=360°,
∴2n∠ABM+2n∠CDM+∠N=360°。
∵∠M=∠ABM+∠CDM,
∴2n∠M+∠N=360°。
∵∠M=m°,
∴∠N=(360 - 2mn)°。
5.
(1)CD 两直线平行,同旁内角互补
(2)∠EPF=∠AEP+∠CFP [解析]如图,过点P作PM//AB,

∵AB//CD,
∴AB//CD//PM,
∴∠AEP=∠MPE,∠CFP=∠MPF,
∴∠EPF=∠MPE+∠MPF=∠AEP+∠CFP,
即∠EPF=∠AEP+∠CFP。
(3)∠AFD=2∠CEB,理由如下:
由
(2),得∠CEB=∠ACE+∠DBE,∠AFD=∠CFB=∠ACF+∠DBF。
∵CE平分∠ACD,BE平分∠ABD,
∴∠ACD=2∠ACE,∠DBF=2∠DBE,
∴∠AFD=2∠CEB。
(4)(360 - 2mn) [解析]
∵∠ABN与∠CDN两个角的平分线相交于点E,
∴∠ABE=$\frac{1}{2}$∠ABN,∠CDE=$\frac{1}{2}$∠CDN。
∵∠ABM=$\frac{1}{n}$∠ABE,∠CDM=$\frac{1}{n}$∠CDE,
∴∠ABE=n∠ABM,∠CDE=n∠CDM,
∴∠ABN=2n∠ABM,∠CDN=2n∠CDM。
由
(1),得∠ABN+∠N+∠CDN=360°,
∴2n∠ABM+2n∠CDM+∠N=360°。
∵∠M=∠ABM+∠CDM,
∴2n∠M+∠N=360°。
∵∠M=m°,
∴∠N=(360 - 2mn)°。
查看更多完整答案,请扫码查看


