第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
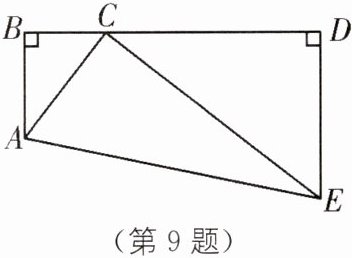
9. 如图,已知点C是线段BD上的一点,∠B= ∠D= 90°,若AB= 3,BC= 2,CD= 6,DE= 4,AE= √65.
(1)求AC,CE的长;
(2)求证:∠ACE= 90°.
(1)求AC,CE的长;
(2)求证:∠ACE= 90°.

答案:
(1)
∵在Rt△ABC中,∠B=90°,AB=3,BC=2,
∴AC=√(AB²+BC²)=√(3²+2²)=√13.
∵在Rt△EDC中,∠D=90°,CD=6,DE=4,
∴CE=√(CD²+DE²)=√(6²+4²)=√52.
(2)
∵AC=√13,CE=√52,AE=√65,
∴AE²=AC²+CE²,
∴∠ACE=90°.
(1)
∵在Rt△ABC中,∠B=90°,AB=3,BC=2,
∴AC=√(AB²+BC²)=√(3²+2²)=√13.
∵在Rt△EDC中,∠D=90°,CD=6,DE=4,
∴CE=√(CD²+DE²)=√(6²+4²)=√52.
(2)
∵AC=√13,CE=√52,AE=√65,
∴AE²=AC²+CE²,
∴∠ACE=90°.
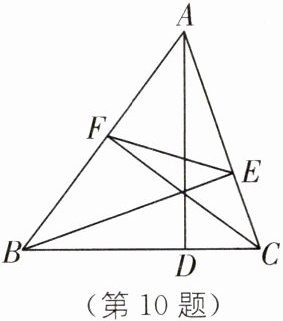
10.(浙江自主招生)如图,设AD,BE,CF为三角形ABC的三条高,若AB= 6,BC= 5,AE-EC= 11/5,则线段BE的长为______
24/5
.
答案:
24/5 [解析]设AE=x,EC=y.
∵BE是△ABC的高,
∴BE⊥AC,
∴BE²=AB² - AE²=BC² - CE²,即36 - x²=25 - y².又x - y=11/5,解得x=18/5,则BE=√(AB² - AE²)=24/5.
∵BE是△ABC的高,
∴BE⊥AC,
∴BE²=AB² - AE²=BC² - CE²,即36 - x²=25 - y².又x - y=11/5,解得x=18/5,则BE=√(AB² - AE²)=24/5.
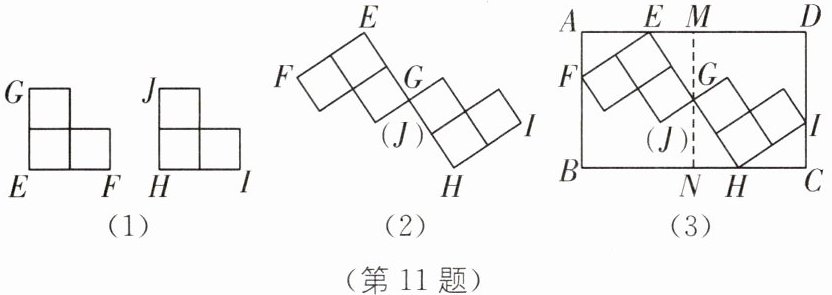
11.(2025·金华金东区期末)在一次综合实践活动中,小明将6个边长为1的小正方形进行如下操作:第一次操作,三个小正方形一组,边重叠拼接成如图(1)所示的2个“L型”;第二次操作,将这2个“L型”顶点G,J重合,并且使得E,G(J),H三点共线,摆放成如图(2)所示的图形;第三次操作,将图(2)中的新图形放置在长方形纸片ABCD中.此时发现,小正方形的顶点E,F,H,I都落在长方形ABCD的各边上,若AB= 3,则BC= ______.

答案:
3+√7 [解析]如图,过点G作MN⊥BC,交BC于点N,交AD于点M.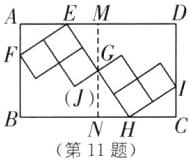
∵∠FEG=90°,
∴∠AEF=∠MGE=90° - ∠MEG,在△AFE和△MEG中,{∠A=∠EMG, ∠AEF=∠MGE, EF=GE,
∴△AFE≌△MEG(AAS),同理可证△NHG≌△CIH(AAS),在△MEG和△NHG中,{∠EMG=∠NHG, ∠MGE=∠NGH, EG=HG,
∴△MEG≌△NHG(AAS),
∴△AFE≌△MEG≌△NHG≌△CIH,
∴设AE=GM=GN=CH=x,AF=EM=NH=CI.
∵AB=MN=GM+GN=2x=3,
∴x=3/2,
∴AE=GM=GN=CH=3/2,
∴BC=BN+NC=AM+NC=AE+EM+NH+CH=2(AE+EM).
∵4EM²=4(EG² - MG²)=7,
∴2EM=√7,
∴BC=3+√7.
3+√7 [解析]如图,过点G作MN⊥BC,交BC于点N,交AD于点M.

∵∠FEG=90°,
∴∠AEF=∠MGE=90° - ∠MEG,在△AFE和△MEG中,{∠A=∠EMG, ∠AEF=∠MGE, EF=GE,
∴△AFE≌△MEG(AAS),同理可证△NHG≌△CIH(AAS),在△MEG和△NHG中,{∠EMG=∠NHG, ∠MGE=∠NGH, EG=HG,
∴△MEG≌△NHG(AAS),
∴△AFE≌△MEG≌△NHG≌△CIH,
∴设AE=GM=GN=CH=x,AF=EM=NH=CI.
∵AB=MN=GM+GN=2x=3,
∴x=3/2,
∴AE=GM=GN=CH=3/2,
∴BC=BN+NC=AM+NC=AE+EM+NH+CH=2(AE+EM).
∵4EM²=4(EG² - MG²)=7,
∴2EM=√7,
∴BC=3+√7.
12. 阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三条边长度之间的关系来判断这个三角形的形状:①若$a^2= b^2+c^2,$则该三角形是直角三角形;②若$a^2>b^2+c^2,$则该三角形是钝角三角形;③若$a^2<b^2+c^2,$则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是$6,6^2= 36<4^2+5^2,$故由③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三边长分别是7,8,9,则该三角形是______三角形;
(2)若一个三角形的三边长分别是5,12,x,且这个三角形是直角三角形,求x的值.
(1)
(2)
(1)若一个三角形的三边长分别是7,8,9,则该三角形是______三角形;
(2)若一个三角形的三边长分别是5,12,x,且这个三角形是直角三角形,求x的值.
(1)
锐角
(2)
当最长边是12时,$x=\sqrt{12^2-5^2}=\sqrt{119}$;当最长边是x时,$x=\sqrt{5^2+12^2}=13$。故x=13或$\sqrt{119}$。
答案:
(1)锐角 [解析]
∵7²+8²=113,9²=81,
∴9²<7²+8²,
∴该三角形是锐角三角形.
(2)当最长边是12时,x=√(12² - 5²)=√119;→容易遗漏x<12这种情况当最长边是x时,x=√(5²+12²)=13.故x=13或√119.归纳总结 本题考查了勾股定理的逆定理和勾股定理,能灵活运用定理进行计算是解题的关键.
(1)锐角 [解析]
∵7²+8²=113,9²=81,
∴9²<7²+8²,
∴该三角形是锐角三角形.
(2)当最长边是12时,x=√(12² - 5²)=√119;→容易遗漏x<12这种情况当最长边是x时,x=√(5²+12²)=13.故x=13或√119.归纳总结 本题考查了勾股定理的逆定理和勾股定理,能灵活运用定理进行计算是解题的关键.
查看更多完整答案,请扫码查看


