第120页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
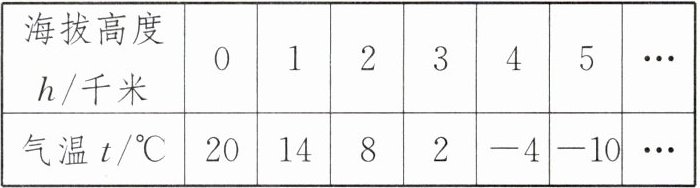
1.(2024·河北张家口桥西区期末)海拔高度 h(千米)与此高度处气温 t(°C)之间有下面的关系:
|海拔高度h/千米|0|1|2|3|4|5|…|
|气温t/°C|20|14|8|2|-4|-10|…|
下列说法错误的是(
A.其中 h 是自变量,t 是因变量
B.海拔越高,气温越低
C.气温 t 与海拔高度 h 的关系式为 t= 20-5h
D.当海拔高度为 8 千米时,其气温是-28°C
|海拔高度h/千米|0|1|2|3|4|5|…|
|气温t/°C|20|14|8|2|-4|-10|…|

下列说法错误的是(
C
).A.其中 h 是自变量,t 是因变量
B.海拔越高,气温越低
C.气温 t 与海拔高度 h 的关系式为 t= 20-5h
D.当海拔高度为 8 千米时,其气温是-28°C
答案:
1.C [解析]A.其中h是自变量,t是因变量,说法正确,不符合题意;B.海拔越高,气温越低,说法正确,不符合题意;C.由表格可知,海拔每升高1千米,气温下降6°C,故气温t与海拔高度h的关系式为t=20−6h,说法错误,符合题意;D.当海拔高度为8千米时,t=20−6×8=−28,说法正确,不符合题意.故选C.
2. 教材 P161 作业题 T1·变式 已知一根弹簧秤不挂物体时弹簧的长度为 7 cm,在弹性限度内,每挂重 1 kg 物体,弹簧伸长 0.5 cm,则挂重后弹簧的长度 y(cm)与所挂物体的质量 x(kg)之间的函数表达式是
y=0.5x+7
.
答案:
y=0.5x+7
3. “十一”期间,小明和父母一起开车到距家 200 km 的景点旅游,出发前,汽车油箱内储油 45 L,当行驶 150 km 时,发现油箱余油量为 30 L.(假设行驶过程中汽车的耗油量是均匀的)
(1)求该车平均每千米的耗油量,并写出行驶路程 x(km)与剩余油量 Q(L)的关系式;
(2)当 x= 280 时,求剩余油量 Q.
(1)求该车平均每千米的耗油量,并写出行驶路程 x(km)与剩余油量 Q(L)的关系式;
(2)当 x= 280 时,求剩余油量 Q.
答案:
3.
(1)该车平均每千米的耗油量为(45−30)÷150=0.1(L),行驶路程x(km)与剩余油量Q(L)的关系式为Q=45−0.1x.
(2)当x=280时,Q=45−0.1×280=17.
故当x=280时,剩余油量Q为17L.
(1)该车平均每千米的耗油量为(45−30)÷150=0.1(L),行驶路程x(km)与剩余油量Q(L)的关系式为Q=45−0.1x.
(2)当x=280时,Q=45−0.1×280=17.
故当x=280时,剩余油量Q为17L.
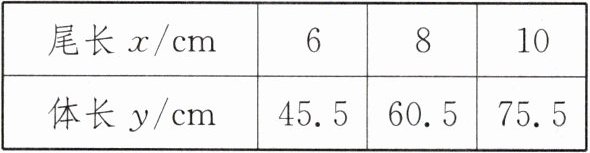
4.(2024·山西中考)生物学研究表明,某种蛇在一定生长阶段,其体长 y(cm)是尾长 x(cm)的一次函数,部分数据如下表所示,则 y 与 x 之间的关系式为(
|尾长x/cm|6|8|10|
|体长y/cm|45.5|60.5|75.5|
A.y= 7.5x+0.5
B.y= 7.5x-0.5
C.y= 15x
D.y= 15x+45.5
A
).|尾长x/cm|6|8|10|
|体长y/cm|45.5|60.5|75.5|

A.y= 7.5x+0.5
B.y= 7.5x-0.5
C.y= 15x
D.y= 15x+45.5
答案:
4.A
5.(广东广州大学附中自主招生)a 是一个正实数,记函数$f(x)= \left[\frac{x+\left[\frac{a}{x}\right]}{2}\right]$,其中[x]是不超过实数 x 的最大整数,如[2.1]= 2,[-2.1]= -3,若 f(5)= 5,则 a 的取值范围是______
5.25≤a<35
.
答案:
5.25≤a<35 [解析]
∵f
(5)=5,
∴5≤5+[$\frac{a}{5}$]÷2<6,
∴5≤[$\frac{a}{5}$]<7,
∴5≤$\frac{a}{5}$<7,
∴25≤a<35.
∵f
(5)=5,
∴5≤5+[$\frac{a}{5}$]÷2<6,
∴5≤[$\frac{a}{5}$]<7,
∴5≤$\frac{a}{5}$<7,
∴25≤a<35.
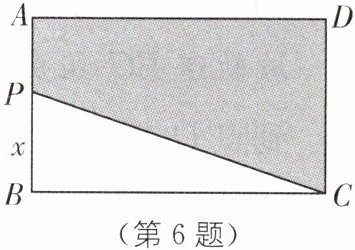
6. 如图,在长方形 ABCD 中,AB= 4,BC= 8.点 P 在 AB 上运动,设 PB= x,图中阴影部分的面积为 y.
(1)求 y 与 x 之间的函数表达式,并直接写出自变量 x 的取值范围;
(2)若阴影部分的面积等于 20,求出此时 PB 的长.
(1)求 y 与 x 之间的函数表达式,并直接写出自变量 x 的取值范围;
(2)若阴影部分的面积等于 20,求出此时 PB 的长.

答案:
6.
(1)在长方形ABCD中,AB=4,BC=8,
∴CD=4.
∵PB=x,
∴AP=4−x.
根据题意,得y=$\frac{1}{2}$×8×(4−x+4)=−4x+32.
∵点P在AB上运动,
∴0≤x≤4,
∴y=−4x+32(0≤x≤4).
(2)若阴影部分的面积等于20,即y=−4x+32=20,
解得x=3,
∴PB=3.
(1)在长方形ABCD中,AB=4,BC=8,
∴CD=4.
∵PB=x,
∴AP=4−x.
根据题意,得y=$\frac{1}{2}$×8×(4−x+4)=−4x+32.
∵点P在AB上运动,
∴0≤x≤4,
∴y=−4x+32(0≤x≤4).
(2)若阴影部分的面积等于20,即y=−4x+32=20,
解得x=3,
∴PB=3.
查看更多完整答案,请扫码查看


