第101页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
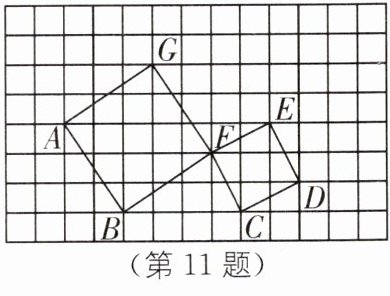
11. 在如图所示的图形中建立平面直角坐标系,使点B,C的坐标分别为(2,0)和(6,0),根据坐标系提供的数据,求:
(1)点A,D,E,F,G的坐标;
(2)△BCF及四边形ABFG的面积.
(1)点A,D,E,F,G的坐标;
(2)△BCF及四边形ABFG的面积.

答案:
(1)如图,以BC所在直线为x轴,过点A且垂直于BC的值为y轴建立平面直角坐标系,

则A(0,3),D(8,1),E(7,3),F(5,2),G(3,5).
(2)S△BCF=$\frac{1}{2}$×4×2=4,S四边形ABFG=5²−4×$\frac{1}{2}$×3×2=13.
(1)如图,以BC所在直线为x轴,过点A且垂直于BC的值为y轴建立平面直角坐标系,

则A(0,3),D(8,1),E(7,3),F(5,2),G(3,5).
(2)S△BCF=$\frac{1}{2}$×4×2=4,S四边形ABFG=5²−4×$\frac{1}{2}$×3×2=13.
12. 中考新考法 新定义问题 (2025·北京师范大学附属中学期中)如图(1),线段AB可以记作a,类似的,以A为起点,以B为终点的有向线段记作$\overrightarrow{AB}或\overrightarrow{a}$. 在平面直角坐标系中,若A($x_1$,$y_1$),B($x_2$,$y_2$),则$\overrightarrow{AB}$= ($x_2 - x_1$,$y_2 - y_1$). 如A(2,1),B(-3,2),则$\overrightarrow{AB}$= (-3-2,2-1)= (-5,1).
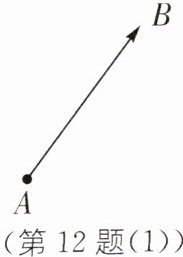
在平面直角坐标系中,设$\overrightarrow{a}$= ($x_1$,$y_1$),$\overrightarrow{b}$= ($x_2$,$y_2$),箭头在字母正上方,不要覆盖前后文字可以如下定义$\overrightarrow{a}$,$\overrightarrow{b}$的运算:
加法:$\overrightarrow{a}+\overrightarrow{b}$= ($x_1 + x_2$,$y_1 + y_2$);
减法:$\overrightarrow{a}-\overrightarrow{b}$= ($x_1 - x_2$,$y_1 - y_2$);
数乘:$k\overrightarrow{a}$= ($kx_1$,$ky_1$)(k为实数);
点乘:$\overrightarrow{a}\bullet\overrightarrow{b}$= $x_1x_2 + y_1y_2$.
对于$\overrightarrow{a}$,$\overrightarrow{b}$,若$\overrightarrow{a}$,$\overrightarrow{b}$所在直线垂直,我们就说$\overrightarrow{a}$,$\overrightarrow{b}$垂直,记为$\overrightarrow{a}\perp\overrightarrow{b}$,若$\overrightarrow{a}\perp\overrightarrow{b}$,则$\overrightarrow{a}\bullet\overrightarrow{b}$= 0. 若$\overrightarrow{a}$,$\overrightarrow{b}$所在直线平行或共线,我们就说$\overrightarrow{a}$,$\overrightarrow{b}$平行,记为$\overrightarrow{a}//\overrightarrow{b}$,若$\overrightarrow{a}//\overrightarrow{b}$,则存在实数k,使得$\overrightarrow{b}= k\overrightarrow{a}$.
根据以上材料回答问题:
(1)若O为坐标原点,点A为(6,2),则$\overrightarrow{OA}$= (
(2)若$\overrightarrow{a}$= (2,3),$\overrightarrow{b}$= (-4,m),其中m为实数,且满足$\overrightarrow{a}//\overrightarrow{b}$,则m=
(3)若$\overrightarrow{a}$= (x-1,2),$\overrightarrow{b}$= (x-2,-3),其中x为实数,则$\overrightarrow{a}\bullet\overrightarrow{b}$=
(4)若$\overrightarrow{a}$= (x,0),$\overrightarrow{b}$= (1,0),$\overrightarrow{c}$= (-1,2x),$\overrightarrow{d}$= (0,1),其中x为实数,且满足$(\overrightarrow{a}+\overrightarrow{c})\perp(\overrightarrow{b}-\overrightarrow{d})$,则x=
(5)如图(2),在平面直角坐标系中,A(0,3),B(-1,0),OB= OD,OA= OC,请用上面材料中的知识,通过运算的方式说明线段AB,CD的位置关系.
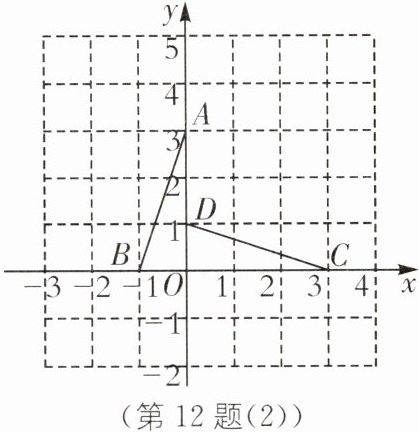
∵A(0,3),B(-1,0),OB=OD,OA=OC,
∴C(3,0),D(0,1),$\overrightarrow{AB}$=(-1-0,0-3)=(-1,-3),$\overrightarrow{CD}$=(0-3,1-0)=(-3,1)
∴$\overrightarrow{AB}\cdot\overrightarrow{CD}$=(-1)×(-3)+(-3)×1=0,∴AB⊥CD.

在平面直角坐标系中,设$\overrightarrow{a}$= ($x_1$,$y_1$),$\overrightarrow{b}$= ($x_2$,$y_2$),箭头在字母正上方,不要覆盖前后文字可以如下定义$\overrightarrow{a}$,$\overrightarrow{b}$的运算:
加法:$\overrightarrow{a}+\overrightarrow{b}$= ($x_1 + x_2$,$y_1 + y_2$);
减法:$\overrightarrow{a}-\overrightarrow{b}$= ($x_1 - x_2$,$y_1 - y_2$);
数乘:$k\overrightarrow{a}$= ($kx_1$,$ky_1$)(k为实数);
点乘:$\overrightarrow{a}\bullet\overrightarrow{b}$= $x_1x_2 + y_1y_2$.
对于$\overrightarrow{a}$,$\overrightarrow{b}$,若$\overrightarrow{a}$,$\overrightarrow{b}$所在直线垂直,我们就说$\overrightarrow{a}$,$\overrightarrow{b}$垂直,记为$\overrightarrow{a}\perp\overrightarrow{b}$,若$\overrightarrow{a}\perp\overrightarrow{b}$,则$\overrightarrow{a}\bullet\overrightarrow{b}$= 0. 若$\overrightarrow{a}$,$\overrightarrow{b}$所在直线平行或共线,我们就说$\overrightarrow{a}$,$\overrightarrow{b}$平行,记为$\overrightarrow{a}//\overrightarrow{b}$,若$\overrightarrow{a}//\overrightarrow{b}$,则存在实数k,使得$\overrightarrow{b}= k\overrightarrow{a}$.
根据以上材料回答问题:
(1)若O为坐标原点,点A为(6,2),则$\overrightarrow{OA}$= (
6
,2
);(2)若$\overrightarrow{a}$= (2,3),$\overrightarrow{b}$= (-4,m),其中m为实数,且满足$\overrightarrow{a}//\overrightarrow{b}$,则m=
-6
;(3)若$\overrightarrow{a}$= (x-1,2),$\overrightarrow{b}$= (x-2,-3),其中x为实数,则$\overrightarrow{a}\bullet\overrightarrow{b}$=
x²−3x−4
;(用含x的式子表示)(4)若$\overrightarrow{a}$= (x,0),$\overrightarrow{b}$= (1,0),$\overrightarrow{c}$= (-1,2x),$\overrightarrow{d}$= (0,1),其中x为实数,且满足$(\overrightarrow{a}+\overrightarrow{c})\perp(\overrightarrow{b}-\overrightarrow{d})$,则x=
-1
;(5)如图(2),在平面直角坐标系中,A(0,3),B(-1,0),OB= OD,OA= OC,请用上面材料中的知识,通过运算的方式说明线段AB,CD的位置关系.

∵A(0,3),B(-1,0),OB=OD,OA=OC,
∴C(3,0),D(0,1),$\overrightarrow{AB}$=(-1-0,0-3)=(-1,-3),$\overrightarrow{CD}$=(0-3,1-0)=(-3,1)
∴$\overrightarrow{AB}\cdot\overrightarrow{CD}$=(-1)×(-3)+(-3)×1=0,∴AB⊥CD.
答案:
(1)6 2 [解析]
∵0(0,0),A(6,$\overrightarrow{OA}$=(6−0,$2-0$)=(6$2$).
(2)−6 [解析]
∵$\overrightarrow{a}//\overrightarrow{b}$,即$\overrightarrow{b}$=k$\overrightarrow{a}$,
∴$\begin{cases}2k=-4\\3k=m\end{cases}$,解得$\begin{cases}k=-2\\m=-6\end{cases}$.
故m=−6.
(3)x²−3x−4 [解析]
∵$\overrightarrow{a}$=(x−1,$2$),$\overrightarrow{b}$=(x−2,−$3$),其中x为实数,
∴$\overrightarrow{a}\cdot\overrightarrow{b}$=(x−$)(x−$2$)+2×(−$3$)=x²−3x−4. (4)−$ [解析]$\overrightarrow{a}$=(x,0),$\overrightarrow{b}$=(1,0),$\overrightarrow{c}$=(−1,2x),$\overrightarrow{d}$=(0,1),$\overrightarrow{a}+\overrightarrow{c}$=(x−1,2x),$\overrightarrow{b}-\overrightarrow{d}$=(1,−1).
∵($\overrightarrow{a}+\overrightarrow{c}$)⊥($\overrightarrow{b}-\overrightarrow{d}$),即($\overrightarrow{a}+\overrightarrow{c}$·($\overrightarrow{b}-\overrightarrow{d}$)=0,
∴x−$1$−2x=0,解得x=−1.
(5)
∵A($0$,$3$),B(−$1$,$0$),OB=OD,OA=OC,
∴C($3$,$0$),D($0$,$),\overrightarrow{AB}$=(−$1$−$0$,$0$−$)=(-1$,$-$,\overrightarrow{CD}$=($0$−$3$,$1$−$0$)=(-3$,$1$)
∴$\overrightarrow{AB}\cdot\overrightarrow{CD}$=(−$1$)×(−$3$)+(−$3$)×$1$=0,
∴AB⊥CD.
(1)6 2 [解析]
∵0(0,0),A(6,$\overrightarrow{OA}$=(6−0,$2-0$)=(6$2$).
(2)−6 [解析]
∵$\overrightarrow{a}//\overrightarrow{b}$,即$\overrightarrow{b}$=k$\overrightarrow{a}$,
∴$\begin{cases}2k=-4\\3k=m\end{cases}$,解得$\begin{cases}k=-2\\m=-6\end{cases}$.
故m=−6.
(3)x²−3x−4 [解析]
∵$\overrightarrow{a}$=(x−1,$2$),$\overrightarrow{b}$=(x−2,−$3$),其中x为实数,
∴$\overrightarrow{a}\cdot\overrightarrow{b}$=(x−$)(x−$2$)+2×(−$3$)=x²−3x−4. (4)−$ [解析]$\overrightarrow{a}$=(x,0),$\overrightarrow{b}$=(1,0),$\overrightarrow{c}$=(−1,2x),$\overrightarrow{d}$=(0,1),$\overrightarrow{a}+\overrightarrow{c}$=(x−1,2x),$\overrightarrow{b}-\overrightarrow{d}$=(1,−1).
∵($\overrightarrow{a}+\overrightarrow{c}$)⊥($\overrightarrow{b}-\overrightarrow{d}$),即($\overrightarrow{a}+\overrightarrow{c}$·($\overrightarrow{b}-\overrightarrow{d}$)=0,
∴x−$1$−2x=0,解得x=−1.
(5)
∵A($0$,$3$),B(−$1$,$0$),OB=OD,OA=OC,
∴C($3$,$0$),D($0$,$),\overrightarrow{AB}$=(−$1$−$0$,$0$−$)=(-1$,$-$,\overrightarrow{CD}$=($0$−$3$,$1$−$0$)=(-3$,$1$)
∴$\overrightarrow{AB}\cdot\overrightarrow{CD}$=(−$1$)×(−$3$)+(−$3$)×$1$=0,
∴AB⊥CD.
查看更多完整答案,请扫码查看


