《2025年实验班提优训练八年级数学上册浙教版》

1. 教材 P112 例1·变式 (2024·西宁中考)不等式组$\left\{\begin{array}{l} x+2＜3,\\ -2x\leqslant1\end{array} \right. $的解集是(B).
A.$x\leqslant-\frac {1}{2}$
B.$-\frac {1}{2}\leqslant x＜1$
C.$x＜1$
D.无解

答案： B [解析] {x + 2 ＜ 3,① -2x ≤ 1,② 解不等式①,得x ＜ 1,解不等式②,得x ≥ -$\frac{1}{2}$,
∴不等式组的解集为 -$\frac{1}{2}$ ≤ x ＜ 1.故选B.　归纳总结　本题考查解不等式组，解题的关键是掌握求不等式公共解集的方法.

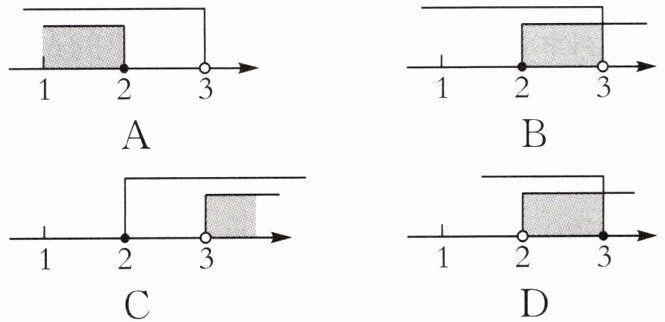
2. (2024·遂宁中考)不等式组$\left\{\begin{array}{l} 3x-2＜2x+1,\\ x\geqslant2\end{array} \right. $的解集在数轴上表示为( ).

答案：
B [解析]由3x - 2 ＜ 2x + 1,得x ＜ 3,　因此不等式组的解集在数轴上表示如图.　　　　　　　　 　故选B

3. (2024·包头中考)若$2m-1,m,4-m$这三个实数在数轴上所对应的点从左到右依次排列,则m的取值范围是(B).
A.$m＜2$
B.$m＜1$
C.$1＜m＜2$
D.$1＜m＜\frac {5}{3}$

答案： B [解析]由题意,得2m - 1 ＜ m ＜ 4 - m,
∴{2m - 1 ＜ m,m ＜ 4 - m,　解得m ＜ 1.故选B.

4. (2024·西藏中考)解不等式组：$\left\{\begin{array}{l} 3x-2＞1,\\ \frac {2x-1}{3}＞x-2,\end{array} \right. $并把解集在数轴上表示出来.

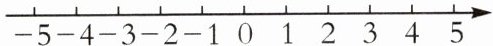
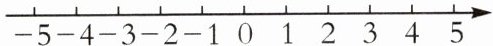
答案：
{3x - 2 ＞ 1,① $\frac{2x - 1}{3}$ ＞ x - 2,② 由①,得x ＞ 1,由②,得x ＜ 5,
∴不等式组的解集为1 ＜ x ＜ 5.　在数轴上表示如图:　　　　　

5. 跨学科 pH检测值 (2025·宁波鄞州区期末)检测游泳池的水质,要求三次检验的pH的平均值不小于7.2,且不大于7.8. 已知第一次pH检测值为7.4,第二次pH检测值在7.0至7.9之间(包含7.0和7.9),若该游泳池检测合格,则第三次pH检测值x的范围是(A).
A.$7.2\leqslant x\leqslant8.1$
B.$7.1\leqslant x\leqslant8.0$
C.$7.2\leqslant x\leqslant8.0$
D.$7.1\leqslant x\leqslant8.1$

答案： A [解析]
∵已知第一次pH检测值为7.4,第二次pH检测值在7.0至7.9之间(包含7.0和7.9)，三次检验的pH 的平均值不小于7.2,且不大于7.8,
∴根据题意，得{7.2 ≤ $\frac{7.4 + 7.0 + x}{3}$,7.8 ≥ $\frac{7.4 + 7.9 + x}{3}$,　解得7.2 ≤ x ≤ 8.1.　故选A.

6. (2025·金华东阳期末)不等式组$\left\{\begin{array}{l} -x\leqslant1,\\ x-3＜1\end{array} \right. $的整数解共有(B).
A.4个
B.5个
C.6个
D.无数个

答案： B [解析]解不等式 -x ≤ 1,得x ≥ -1,　解不等式x - 3 ＜ 1,得x ＜ 4,　所以不等式组的解集是 -1 ≤ x ＜ 4，　即不等式组的整数解有 -1,0,1,2,3,共5个.故选B.

7. (2025·杭州外国语学校期末)已知关于x的不等式组$\left\{\begin{array}{l} x-m\geqslant0,\\ 3x-n＜0\end{array} \right. $的整数解为1,2(其中m,n为整数),则满足条件的(m,n)共有(C).
A.1对
B.2对
C.3对
D.4对

答案： C [解析]解不等式x - m ≥ 0,得x ≥ m,　解不等式3x - n ＜ 0得,x ＜ $\frac{n}{3}$,
∵不等式组的整数解为1,2,
∴0 ＜ m ≤ 1,且2 ＜ $\frac{n}{3}$ ≤ 3,则0 ＜ m ≤ 1,6 ＜ n ≤ 9.　又m,n为整数,
∴m = 1,n = 7,8,9,
∴满足条件的(m,n)共有3对.故选C.

8. (2024·南充中考)若关于x的不等式组$\left\{\begin{array}{l} 2x-1＜5,\\ x＜m+1\end{array} \right. $的解集为x＜3,则m的取值范围是(B).
A.$m＞2$
B.$m\geqslant2$
C.$m＜2$
D.$m\leqslant2$

答案： B [解析]
∵关于x的不等式组{2x - 1＜5,x＜m+1}的解集为x＜3,
∴m + 1 ≥ 3,
∴m ≥ 2.故选B.

9. 方程思想 (2025·重庆一中期末)若关于x的不等式组$\left\{\begin{array}{l} 7x-a\geqslant1,\\ \frac {x+5}{3}\geqslant x-1\end{array} \right. $有且仅有4个整数解,且关于m,n的二元一次方程组$\left\{\begin{array}{l} m+2n= 3,\\ 2m-2n= a\end{array} \right. $的解为整数,则所有满足条件的整数a的和为______6.

答案： 6 [解析] {7x - a ≥ 1,① $\frac{x + 5}{3}$ ≥ x - 1,②　解不等式①,得x ≥ $\frac{a + 1}{7}$,解不等式②,得x ≤ 4.
∵此不等式组有且仅有4个整数解，
∴0 ＜ $\frac{a + 1}{7}$ ≤ 1,解得 -1 ＜ a ≤ 6.　解方程组{m + 2n = 3,2m - 2n = a}得{m = $\frac{a + 3}{3}$,n = $\frac{6 - a}{6}$}.
∵此方程组的解为整数,
∴满足条件的整数有0,6,
∴所有满足条件的整数a的和为6.

10. 教材 P119 目标与评定 T7·变式 (2025·宁波蛟川书院期末)若关于x的不等式组$\left\{\begin{array}{l} 2x+a\geqslant0,\\ x-2a＜0\end{array} \right. $的整数解有且只有一个,则a的取值范围是0 ＜ a ≤ $\frac{1}{2}$.

答案： 0 ＜ a ≤ $\frac{1}{2}$ [解析]解不等式2x + a ≥ 0,得x ≥ -$\frac{a}{2}$,　解不等式x - 2a ＜ 0,得x ＜ 2a,
∴ -$\frac{a}{2}$ ≤ x ＜ 2a,
∴当a = 0时，此不等式组无解，
∴a ≠ 0,则 -$\frac{a}{2}$与2a异号，
∴此不等式组的整数解为0,则 -1 ＜ -$\frac{a}{2}$ ＜ 0且0 ＜ 2a ≤ $\frac{1}{2}$.