《2025年实验班提优训练八年级数学上册浙教版》

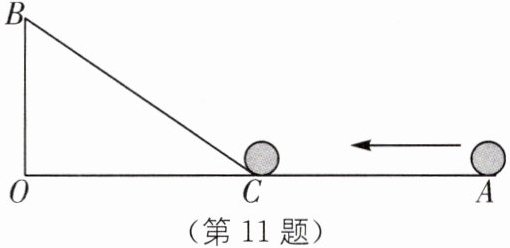
11.(2024·江苏徐州铜山区期中)如图,$\angle AOB= 90^{\circ}$,$OA= 45\ \text{cm}$,$OB= 15\ \text{cm}$,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少？
]

答案：
∵小球滚动的速度与机器人行走的速度相等，运动时间相等,
∴BC=CA,设AC为xcm,则OC=(45−x)cm,
由勾股定理,得OB²+OC²=BC²,
∴15²+(45−x)²=x²,解得x=25.
故如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是25cm.

12. 中考新考法 新定义问题 (2025·江苏扬州广陵区期末)定义：在$\triangle ABC$中,若$BC= a$,$AC= b$,$AB= c$,a,b,c满足$ac+a^{2}= b^{2}$,则称这个三角形为“类勾股三角形”.请根据以上定义解决下列问题：
(1)如图(1)所示,若等腰三角形ABC是“类勾股三角形”,$AB= BC$,$AC＞AB$,求$\angle A$的度数；
(2)如图(2)所示,在$\triangle ABC$中,$\angle B= 2\angle A$,且$\angle C＞\angle A$,求证：$\triangle ABC$为“类勾股三角形”.小明同学想到可以在AB上找一点D使得$AD= CD$,再作$CE\perp BD$,请你帮助小明完成证明过程.
]

答案：

(1)
∵AB=BC,AC＞AB,
∴a=c,b＞c.
∵△ABC是类勾股三角形,
∴ac+a²=b²,
∴c²+a²=b²,
∴△ABC是等腰直角三角形,
∴∠A=45°.
(2)如图,在AB上找一点D使得AD=CD,再作CE ⊥BD,

∴∠A=∠ACD,
∴∠CDB=∠ACD+∠A=2∠A.
∵∠B=2∠A,
∴∠CDB=∠B,
∴CD=CB=a,
∴AD=CD=a,
∴DB=AB−AD=c−a.
∵CE⊥AB,
∴DE=BE=$\frac{1}{2}$(c−a),
∴AE=AD+DE=a+$\frac{1}{2}$(c−a)=$\frac{1}{2}$(c+a).
在Rt△ACE中,CE²=AC²−AE²=b²−[$\frac{1}{2}$(c+a)]²,
在Rt△BCE中,CE²=BC²−BE²=a²−[$\frac{1}{2}$(c−a)]²,
∴b²−[$\frac{1}{2}$(c+a)]²=a²−[$\frac{1}{2}$(c−a)]²,
∴b²=ac+a²,
∴△ABC是“类勾股三角形”

13.(2024·陕西中考)如图,在$\triangle ABC$中,$AB= AC$,E是边AB上一点,连结CE,在BC的右侧作$BF// AC$,且$BF= AE$,连结CF.若$AC= 13$,$BC= 10$,则四边形EBFC的面积为______.
]

答案：
60　[解析]
∵AB=AC,
∴∠ABC=∠ACB.
∵BF//AC,
∴∠ACB=∠CBF,
∴∠ABC=∠CBF,
∴BC平分∠ABF.
如图,过点C作CM⊥AB于点M,CN⊥BF于点N,

则CM=CN.
→角平分线上的点到角两边的距离相等
∵S△ACE=$\frac{1}{2}$AE·CM,S△CBF=$\frac{1}{2}$BF·CN,且BF=AE,
∴S△CBF=S△ACE,
∴四边形EBFC的面积=S△CBF+S△CBE=S△ACE+S△CBE=S△CBA.
∵AC=13,
∴AB=13.设AM=x,则BM=13−x,
由勾股定理,得CM²=AC²−AM²=BC²−BM²,
∴13²−x²=10²−(13−x)²,解得x=$\frac{119}{13}$,
∴CM=$\sqrt{13²-(\frac{119}{13})²}$=$\frac{120}{13}$,
∴S△CBA=$\frac{1}{2}$AB·CM=60,
∴四边形EBFC的面积为60.