第132页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
9. 将军饮马模型 (湖北武汉六中自主招生)如图,$A(0,1),M(3,2),N(4,4)$,动点P从点A出发,沿y轴以每秒1个单位长度的速度向正方向移动,过点P的直线$l:y= -x+b$也随之移动,设移动时间为t秒.
(1)若直线l与线段MN有交点,确定t的取值范围;
(2)设直线l与x轴交点为Q,若$QM+QN$取得最小值,求此时直线l的函数表达式.
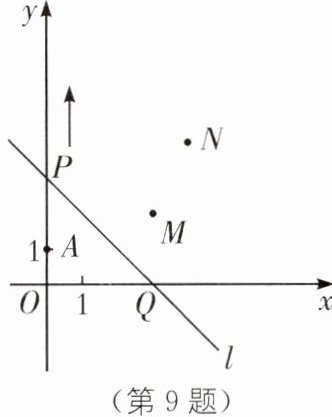
(1)若直线l与线段MN有交点,确定t的取值范围;
(2)设直线l与x轴交点为Q,若$QM+QN$取得最小值,求此时直线l的函数表达式.

答案:
9.
(1)当直线 l 过点 M(3,2)时,2=-3+b,解得 b=5,
∴5=1+t,
∴t=4;当直线 l 过点 N(4,4)时,4=-4+b,解得 b=8,
∴8=1+t,
∴t=7,
∴当直线 l 与线段 MN 有交点时,t 的取值范围为 4≤t≤7.
(2)如图,作点 M关于 x 轴的对称点 M'(3,-2),连结 M'N,交 x 轴于点 Q,此时 MQ+NQ 的值最小,最小值为 M'N.设直线 M'N 的表达式为 y=kx+n,把 M'(3,-2),N(4,4)代入,得{3k+n=-2,4k+n=4},解得{k=6,n=-20},
∴直线 M'N 的表达式为 y=6x-20 .当 y=0 时,6x-20=0,解得$ x=\frac{10}{3},$
∴$Q(\frac{10}{3},0).$把$ Q(\frac{10}{3},0)$代入 y=-x+b ,得$ 0=-\frac{10}{3}+b,$解得$ b=\frac{10}{3}.$
∴直线 l 的函数表达式为$ y=-x+\frac{10}{3}.$
9.
(1)当直线 l 过点 M(3,2)时,2=-3+b,解得 b=5,
∴5=1+t,
∴t=4;当直线 l 过点 N(4,4)时,4=-4+b,解得 b=8,
∴8=1+t,
∴t=7,
∴当直线 l 与线段 MN 有交点时,t 的取值范围为 4≤t≤7.

(2)如图,作点 M关于 x 轴的对称点 M'(3,-2),连结 M'N,交 x 轴于点 Q,此时 MQ+NQ 的值最小,最小值为 M'N.设直线 M'N 的表达式为 y=kx+n,把 M'(3,-2),N(4,4)代入,得{3k+n=-2,4k+n=4},解得{k=6,n=-20},
∴直线 M'N 的表达式为 y=6x-20 .当 y=0 时,6x-20=0,解得$ x=\frac{10}{3},$
∴$Q(\frac{10}{3},0).$把$ Q(\frac{10}{3},0)$代入 y=-x+b ,得$ 0=-\frac{10}{3}+b,$解得$ b=\frac{10}{3}.$
∴直线 l 的函数表达式为$ y=-x+\frac{10}{3}.$
10. (1)一次函数$y= 2x+1$的图象上每个点的横坐标不变,纵坐标都增加1个单位长度后,得到的函数图象表达式是______
(2)①一次函数$y= 2x+1$的图象上每个点的横坐标扩大2倍,纵坐标不变,得到的函数图象表达式是(
A.$y= 4x+1$
B.$y= x+1$
C.$y= x+\frac {1}{2}$
②一次函数$y_{1}= k_{1}x+b_{1}$的图象上每个点的横坐标扩大2倍,纵坐标不变,得到的函数图象表达式是$y_{2}= k_{2}x+b_{2}$,求$\frac {k_{1}}{k_{2}}+2(b_{1}-b_{2})$的值.
y=2x+2
.(2)①一次函数$y= 2x+1$的图象上每个点的横坐标扩大2倍,纵坐标不变,得到的函数图象表达式是(
B
).A.$y= 4x+1$
B.$y= x+1$
C.$y= x+\frac {1}{2}$
②一次函数$y_{1}= k_{1}x+b_{1}$的图象上每个点的横坐标扩大2倍,纵坐标不变,得到的函数图象表达式是$y_{2}= k_{2}x+b_{2}$,求$\frac {k_{1}}{k_{2}}+2(b_{1}-b_{2})$的值.
2
答案:
10.
(1)y=2x+2
(2)①B [解析]函数 y=2x+1 中,当 x=1时,y=3,当 x=-1 时,y=-1.
∵一次函数 y=2x+1 的图象过点 (1 ,3),(-1,-1),
∴横坐标扩大 2 倍 ,纵坐标不变后,得到(2 ,3),(-2,-1),把(2,3),(-2,-1)代入 y=kx+b,得{2k+b=3,-2k+b=-1},解得{k=1,b=1},
∴一次函数 y=2x+1 的图象上每个点的横坐标扩大 2 倍,纵坐标不变,得到的函数图象表达式是 y=x+1.②一次函数 y₁=k₁x+b₁ 的图象上每个点的横坐标扩大 2 倍,纵坐标不变,得到的函数图象表达式是 y₂=k₂x+b₂,则 b₁=b₂,k₁=2k₂.
∴$\frac{k₁}{k₂}+2(b₁-b₂)=\frac{2k₂}{k₂}=2.$
(1)y=2x+2
(2)①B [解析]函数 y=2x+1 中,当 x=1时,y=3,当 x=-1 时,y=-1.
∵一次函数 y=2x+1 的图象过点 (1 ,3),(-1,-1),
∴横坐标扩大 2 倍 ,纵坐标不变后,得到(2 ,3),(-2,-1),把(2,3),(-2,-1)代入 y=kx+b,得{2k+b=3,-2k+b=-1},解得{k=1,b=1},
∴一次函数 y=2x+1 的图象上每个点的横坐标扩大 2 倍,纵坐标不变,得到的函数图象表达式是 y=x+1.②一次函数 y₁=k₁x+b₁ 的图象上每个点的横坐标扩大 2 倍,纵坐标不变,得到的函数图象表达式是 y₂=k₂x+b₂,则 b₁=b₂,k₁=2k₂.
∴$\frac{k₁}{k₂}+2(b₁-b₂)=\frac{2k₂}{k₂}=2.$
11. (2023·绍兴中考)一条笔直的路上依次有M,P,N三地,其中M,N两地相距1000米,甲、乙两机器人分别从M,N两地同时出发,去目的地N,M,匀速而行.图中OA,BC分别表示甲、乙机器人离M地的距离y(米)与行走时间x(分钟)的函数关系图象.
(1)求OA所在直线的表达式.
(2)出发后甲机器人行走多少时间,与乙机器人相遇?
(3)甲机器人到P地后,再经过1分钟乙机器人也到P地,求P,M两地间的距离.
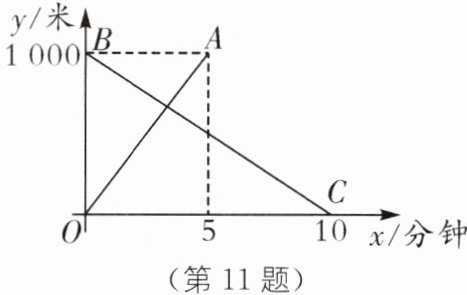
(1)求OA所在直线的表达式.
(2)出发后甲机器人行走多少时间,与乙机器人相遇?
(3)甲机器人到P地后,再经过1分钟乙机器人也到P地,求P,M两地间的距离.

答案:
11.
(1)由题中图象可知,OA 所在直线为正比例函数,
∴设 y=kx.
∵A(5,1000),
∴1000=5k,
∴k=200,
∴OA 所在直线的表达式为 y=200x.
(2)由题图可知,甲机器人速度为 1000÷5=200(米/分钟),乙机器人速度为 1000÷10=100(米/分钟),两人相遇时间为$\frac{1000}{100+200}=\frac{10}{3}($分钟).故出发后甲机器人行走$\frac{10}{3}$分钟,与乙机器人相遇.
(3)设甲机器人行走 t 分钟时到 P 地,P 地与 M 地距离为 200t 米,则乙机器人行走(t+1)分钟后到 P 地,P 地与 M 地距离为 1000-100(t+1),由 200t=1000-100(t+1),解得 t=3.
∴200t=600.故 P,M 两地间的距离为 600 米.
(1)由题中图象可知,OA 所在直线为正比例函数,
∴设 y=kx.
∵A(5,1000),
∴1000=5k,
∴k=200,
∴OA 所在直线的表达式为 y=200x.
(2)由题图可知,甲机器人速度为 1000÷5=200(米/分钟),乙机器人速度为 1000÷10=100(米/分钟),两人相遇时间为$\frac{1000}{100+200}=\frac{10}{3}($分钟).故出发后甲机器人行走$\frac{10}{3}$分钟,与乙机器人相遇.
(3)设甲机器人行走 t 分钟时到 P 地,P 地与 M 地距离为 200t 米,则乙机器人行走(t+1)分钟后到 P 地,P 地与 M 地距离为 1000-100(t+1),由 200t=1000-100(t+1),解得 t=3.
∴200t=600.故 P,M 两地间的距离为 600 米.
查看更多完整答案,请扫码查看


