《2025年实验班提优训练八年级数学上册浙教版》

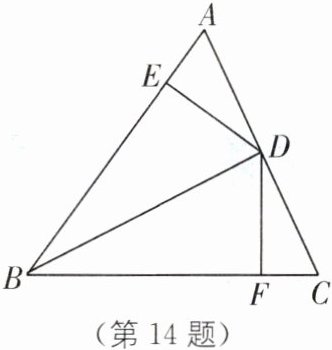
14. (2024·金华金东区期中)如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为E,F.
(1)求证：DE= DF；
(2)若△ABC的面积为70,AB= 16,DE= 5,求BC的长.

答案：
(1)
∵DE⊥AB，DF⊥BC，
∴∠BED=∠BFD=90°.
∵BD是△ABC的角平分线，
∴∠ABD=∠CBD.
又BD=BD，
∴△EBD≌△FBD，
∴DE=DF.
(2)由
(1)可知，S△ABD=$\frac{1}{2}$AB·DE=40.
∵S△ABC=70，
∴S△BCD=$\frac{1}{2}$BC·DF=S△ABC-S△ABD=70-40=30，
∴BC=12.

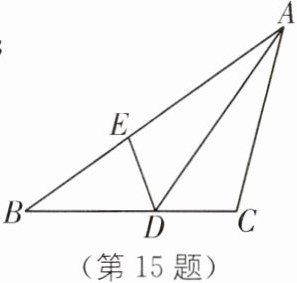
15. (2025·新疆乌鲁木齐月考)已知：如图,在△ABC中,AD平分∠BAC. 在AB上截取AE= AC,连结DE. 若BC= 6 cm, BE= 3 cm.
(1)求证：△AED≌△ACD；
(2)求△BED的周长.

答案：
(1)
∵AD平分∠BAC，
∴∠EAD=∠CAD.
在△AED和△ACD中，
AE=AC，
∠EAD=∠CAD，
AD=AD，
∴△AED≌△ACD(SAS).
(2)由
(1)可知，△AED≌△ACD，
∴ED=CD.
∵BC=6 cm，BE=3 cm，
∴BD+ED=BD+CD=BC=6 cm，
∴BD+ED+BE=6+3=9(cm)，
∴△BED的周长是9 cm.

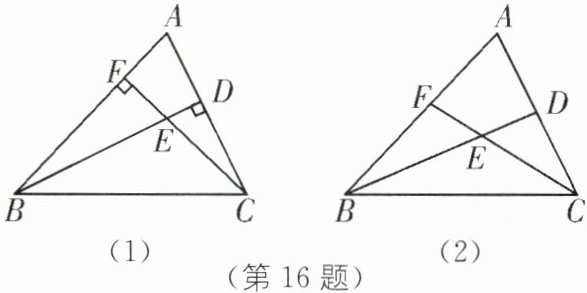
16. 在△ABC中,点D,F分别为线段AC,AB上两点,连结BD,CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图(1)所示,试说明∠BAC+∠BEC= 180°；
(2)若BD平分∠ABC,CF平分∠ACB,如图(2)所示,试说明此时∠BAC与∠BEC的数量关系；
(3)在(2)的条件下,若∠BAC= 60°,试说明EF= ED.

答案：
(1)
∵BD⊥AC，CF⊥AB，
∴∠DCE+∠DEC=∠DCE+∠BAC=90°.
∴∠DEC=∠BAC. 又∠DEC+∠BEC=180°，
∴∠BAC+∠BEC=180°.
(2)∠BEC=90°+$\frac{1}{2}$∠BAC. 理由如下：
∵BD平分∠ABC，CF平分∠ACB，
∴∠EBC=$\frac{1}{2}$∠ABC，∠ECB=$\frac{1}{2}$∠ACB，
∴∠BEC=180°-(∠EBC+∠ECB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-∠BAC)=90°+$\frac{1}{2}$∠BAC.
(3)如图，作∠BEC的平分线EM交BC于点M.
∵∠BAC=60°，
∴∠BEC=90°+$\frac{1}{2}$∠BAC=120°.
∴∠FEB=∠DEC=60°.
∵EM平分∠BEC，
∴∠BEM=60°.
在△FBE与△MBE中，
∠EBF=∠EBM，
BE=BE，
∠FEB=∠MEB，
∴△FBE≌△MBE(ASA).
∴EF=EM. 同理，可得DE=EM，
∴EF=DE.

17. 一题多问 中考新考法 存在性问题 (2025·绍兴嵊州三界片期中)如图,在长方形ABCD中,AB= CD= 8 cm,BC= 14 cm,点P从点B出发,以2 cm/s的速度沿BC向点C运动,设点P的运动时间为t秒.
(1)BP= 2t cm.(用含t的代数式表示)
(2)当t为何值时,△ABP≌△DCP？
若△ABP≌△DCP，则BP=CP，即2t=14-2t，解得t=$\frac{7}{2}$. 故t=$\frac{7}{2}$时，△ABP≌△DCP.
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/s的速度沿CD向点D运动,是否存在这样的v值,使得△ABP与△PQC全等？若存在,请求出v的值；若不存在,请说明理由.
①当△ABP≌△PCQ时，
∴BP=CQ，AB=PC.
∵AB=8 cm，
∴PC=8 cm，
∴BP=BC-PC=14-8=6(cm)，
∴2t=6，解得t=3，
∴CQ=BP=6 cm，即3v=6，解得v=2；
②当△ABP≌△QCP时，
∴BA=CQ，PB=PC，
∴BP=PC=$\frac{1}{2}$BC=7 cm，
∴2t=7，解得t=$\frac{7}{2}$.
∴CQ=BA=8，即$\frac{7}{2}$v=8，解得v=$\frac{16}{7}$.
综上所述，当v的值为2或$\frac{16}{7}$时，△ABP与△PQC全等.

答案：
(1)2t [解析]点P从点B出发，以2 cm/s的速度沿BC向点C运动，点P的运动时间为t秒时，BP=2t cm.
(2)若△ABP≌△DCP，则BP=CP，即2t=14-2t，解得t=$\frac{7}{2}$. 故t=$\frac{7}{2}$时，△ABP≌△DCP.
(3)①当△ABP≌△PCQ时，
∴BP=CQ，AB=PC.
∵AB=8 cm，
∴PC=8 cm，
∴BP=BC-PC=14-8=6(cm)，
∴2t=6，解得t=3，
∴CQ=BP=6 cm，即3v=6，解得v=2；
②当△ABP≌△QCP时，
∴BA=CQ，PB=PC，
∴BP=PC=$\frac{1}{2}$BC=7 cm，
∴2t=7，解得t=$\frac{7}{2}$.
∴CQ=BA=8，即$\frac{7}{2}$v=8，解得v=$\frac{16}{7}$.
综上所述，当v的值为2或$\frac{16}{7}$时，△ABP与△PQC全等.