《2025年实验班提优训练八年级数学上册浙教版》

9. 已知∠ACB= 90°,CD⊥AB,AB= 13,BC= 12,AC= 5,画出图形并求：
(1)△ABC 的面积；
(2)CD 的长.

答案：
如图所示.
　　　　　　　
(1)S△ABC=$\frac{1}{2}$AC·BC=$\frac{1}{2}$×5×12=30.
(2)
∵$\frac{AB·CD}{2}$=S△ABC,
∴CD=$\frac{2S△ABC}{AB}$=$\frac{60}{13}$.

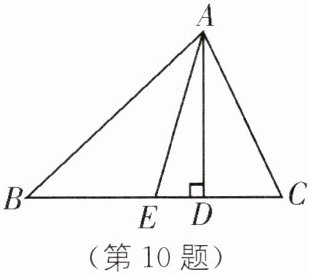
10. 如图,已知 AE,AD 分别为△ABC 的边 BC 上的中线和高线,且 AB= 11 cm,AC= 7 cm.
(1)△ABE 的周长比△ACE 的周长长多少厘米？
(2)△ABE 的面积是 S△ABE,△ACE 的面积是 S△ACE,你能得出 S△ABE 与 S△ACE 的大小关系吗？

答案：
(1)
∵AE是△ABC的中线,
∴BE=CE.
∵△ABE的周长=AB+BE+AE,△ACE的周长=AC+CE+AE=AC+BE+AE,
∴△ABE的周长−△ACE的周长=(AB+BE+AE)−(AC+BE+AE)=AB−AC=11−7=4(cm).故△ABE的周长比△ACE 的周长长4cm.
(2)
∵S△ABE=$\frac{1}{2}$BE·AD,S△ACE=$\frac{1}{2}$CE·AD=$\frac{1}{2}$BE·AD,
∴S△ABE=S△ACE.

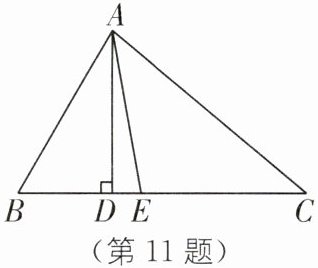
11.(2024·杭州滨江区期末)如图,在△ABC 中,AD 是△ABC 的高线,AE 是△ABC 的角平分线.
(1)若∠B= 60°,∠C= 40°,求∠DAE 的度数；
(2)若∠B= α,∠C= β(α＞β),请直接写出∠DAE 的度数.(用含 α,β 的代数式表示)

答案：
(1)
∵AD是△ABC的高线，
∴∠ADB=90°.
∵∠B=60°,∠C=40°,
∴∠BAD=180°−∠B−∠ADB=30°,
　∠BAC=180°−∠B−∠C=80°.
∵AE是△ABC的角平分线，
∴∠BAE=$\frac{1}{2}$∠BAC=40°,
∴∠DAE=∠BAE−∠BAD=10°.
(2)
∵AD是△ABC的高线，
∴∠ADB=90°.
∵∠B=α,∠C=β,
∴∠BAD=180°−∠B−∠ADB=90°−α,
　∠BAC=180°−∠B−∠C=180°−α−β.
∵AE是△ABC的角平分线，
∴∠BAE=$\frac{1}{2}$∠BAC=90°−$\frac{1}{2}$α−$\frac{1}{2}$β,
∴∠DAE=∠BAE−∠BAD=$\frac{1}{2}$α−$\frac{1}{2}$β.

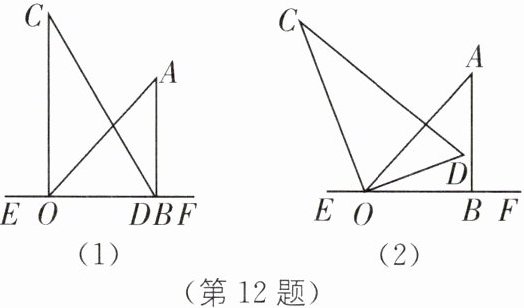
12. 分类讨论思想 将一副三角板按照如图(1)所示的位置放置在直线 EF 上,现将含 30°角的三角板 OCD 绕点 O 逆时针旋转 180°,在旋转过程中,完成以下问题.
(1)如图(2),当 OD 平分∠AOB 时,求∠BOC 的度数；
(2)当 OC 在直线 EF 上方,且∠COE= 30°时,求∠AOD 的度数；
(3)若∠BOC= α,∠AOD= β,请直接写出 α,β 满足的数量关系.

精题详解

答案：

(1)根据题意,得∠AOB=45°,∠COD=90°.
∵OD平分∠AOB，
∴∠BOD=∠AOD=$\frac{1}{2}$∠AOB=22.5°,
∴∠BOC=∠COD+∠BOD=90°+22.5°=112.5°.
(2)如图.
　　　　　　　
∵∠BOA+∠AOD+∠DOC+∠COE=180°,
∴∠AOD=180°−90°−45°−30°=15°.
(3)当∠AOD在∠AOB内部时,α+β=45°+90°=135°;
　　当∠AOD在∠AOB外部时，
　①旋转角大于等于45°而小于90°,α−β=135°;
　②旋转角大于等于90°而小于180°,α+β=225°.