《2025年实验班提优训练八年级数学上册浙教版》

8. (2025·宁波鄞州区期末改编)已知 $ y $ 是 $ x $ 的一次函数,且当 $ x= 2 $ 时,$ y= 0 $;当 $ x= -4 $ 时,$ y= 8 $.
(1)求这个一次函数的表达式；
(2)当 $ x= -\frac{1}{2} $ 时,求函数 $ y $ 的值.

答案： 8.
(1)设y=kx+b,将点(2,0),(-4,8)代入，得{2k+b=0,-4k+b=8,解得{k=-43,b=83,
∴这个一次函数の表达式为y=-43x+83.
(2)将x=-12代入y=-43x+83，得y=-43×(-12)+83=103

9. A,B 两家超市平时以同样的价格出售相同的商品. 暑假期间两家超市都进行促销活动,促销方式如下：
A 超市：一次购物不超过 300 元的打 9 折,超过 300 元后的价格部分打 7 折；
B 超市：一次购物不超过 100 元的按原价,超过 100 元后的价格部分打 8 折.
例如,一次购物的商品原价为 500 元,去 A 超市的购物金额为 $ 300 × 0.9+(500-300) × 0.7= 410 $(元)；去 B 超市的购物金额为 $ 100+(500-100) × 0.8= 420 $(元).
(1)设商品原价为 $ x $ 元,购物金额为 $ y $ 元,分别就两家超市的促销方式写出 $ y $ 关于 $ x $ 的函数表达式.
(2)促销期间,若小刚一次购物的商品原价超过 200 元,他去哪家超市购物更省钱？请说明理由.

答案： 1. （1）
A超市**：
当$0\lt x\leqslant300$时，$y = 0.9x$；
当$x\gt300$时，$y=300×0.9+(x - 300)×0.7=0.7x+60$。
所以$y_{A}=\begin{cases}0.9x(0\lt x\leqslant300)\\0.7x + 60(x\gt300)\end{cases}$。
B超市**：
当$0\lt x\leqslant100$时，$y=x$；
当$x\gt100$时，$y = 100+(x - 100)×0.8=0.8x+20$。
所以$y_{B}=\begin{cases}x(0\lt x\leqslant100)\\0.8x + 20(x\gt100)\end{cases}$。
2. （2）
因为小刚一次购物的商品原价超过$200$元，所以分情况讨论：
当$200\lt x\leqslant300$时：
$y_{A}=0.9x$，$y_{B}=0.8x + 20$。
令$y_{A}-y_{B}=0.9x-(0.8x + 20)=0.1x-20$。
当$y_{A}-y_{B}=0$时，$0.1x-20 = 0$，解得$x = 200$（舍去）；
当$y_{A}-y_{B}\gt0$时，$0.1x-20\gt0$，解得$x\gt200$，此时$y_{A}\gt y_{B}$；
当$y_{A}-y_{B}\lt0$时，$0.1x-20\lt0$，解得$x\lt200$（舍去）。
当$x\gt300$时：
$y_{A}=0.7x + 60$，$y_{B}=0.8x + 20$。
令$y_{A}-y_{B}=(0.7x + 60)-(0.8x + 20)=-0.1x + 40$。
当$y_{A}-y_{B}=0$时，$-0.1x + 40=0$，解得$x = 400$；
当$y_{A}-y_{B}\gt0$时，$-0.1x + 40\gt0$，解得$x\lt400$，此时$y_{A}\gt y_{B}$；
当$y_{A}-y_{B}\lt0$时，$-0.1x + 40\lt0$，解得$x\gt400$，此时$y_{A}\lt y_{B}$。
综上，当$200\lt x\lt400$时，去$B$超市购物更省钱；当$x = 400$时，去$A$、$B$两家超市购物一样；当$x\gt400$时，去$A$超市购物更省钱。

10. (2023·永州中考)小明观察到一个水龙头因损坏而不断地向外滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如表的一组数据：

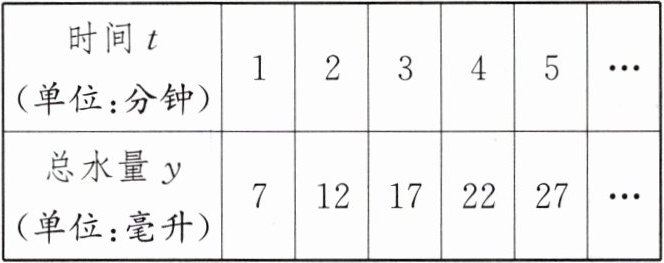
(1)探究：根据上表中的数据,请判断 $ y= \frac{k}{t} $ 和 $ y= kt+b $($ k $,$ b $ 为常数)哪一个能正确反映总水量 $ y $ 与时间 $ t $ 的函数关系？并求出 $ y $ 关于 $ t $ 的函数表达式.
$ y= kt+b $能正确反映总水量$ y $与时间$ t $的函数关系，$ y=5t+2 $
(2)应用：
①请你估算小明在第 20 分钟测量时量筒的总水量是多少毫升.
102毫升
②一个人一天大约饮用 1500 毫升水,请你估算这个水龙头一个月(按 30 天计)的漏水量可供一人饮用多少天.
144天

答案： 1. （1）
解：判断函数关系：
对于$y = \frac{k}{t}$，若$t = 1,y = 7$，则$k = 7$，此时$y=\frac{7}{t}$，当$t = 2$时，$y=\frac{7}{2}=3.5\neq12$，所以$y=\frac{k}{t}$不能正确反映总水量$y$与时间$t$的函数关系。
对于$y = kt + b$，把$\left\{\begin{array}{l}t = 1,y = 7\\t = 2,y = 12\end{array}\right.$代入$y=kt + b$得：
$\begin{cases}k + b=7\\2k + b = 12\end{cases}$。
用$2k + b = 12$减去$k + b=7$，即$(2k + b)-(k + b)=12 - 7$。
展开得$2k + b - k - b=5$，解得$k = 5$。
把$k = 5$代入$k + b=7$，得$5 + b=7$，解得$b = 2$。
当$t = 3$时，$y=5×3 + 2=17$；当$t = 4$时，$y=5×4+2 = 22$；当$t = 5$时，$y=5×5 + 2=27$，均满足表中数据。
所以$y = kt + b$能正确反映总水量$y$与时间$t$的函数关系，函数表达式为$y = 5t+2$。
2. （2）
①
解：当$t = 20$时，把$t = 20$代入$y = 5t+2$，得$y=5×20 + 2$。
$y=100 + 2=102$（毫升）。
②
解：当$t = 60×24$时，$y=5×60×24+2=7200 + 2=7202$（毫升）。
一个月（$30$天）的漏水量为$7202×30$毫升。
可供一人饮用的天数为$\frac{7202×30}{1500}\approx144$（天）。
综上，（1）$y = kt + b$能正确反映，$y = 5t+2$；（2）①$102$毫升；②$144$天。