第96页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
4. (2024·黑龙江中考)为了增强学生的体质,某学校倡导学生在大课间开展踢毽子活动,需购买甲、乙两种品牌毽子. 已知购买甲种品牌毽子 10 个和乙种品牌毽子 5 个共需 200 元;购买甲种品牌毽子 15 个和乙种品牌毽子 10 个共需 325 元.
(1)购买一个甲种品牌毽子和一个乙种品牌毽子各需要多少元?
(2)若购买甲、乙两种品牌毽子共花费 1000 元,甲种品牌毽子数量不低于乙种品牌毽子数量的 5 倍且不超过乙种品牌毽子数量的 16 倍,则有几种购买方案?
(3)若商家每售出一个甲种品牌毽子利润是 5 元,每售出一个乙种品牌毽子利润是 4 元,在(2)的条件下,学校如何购买毽子商家获得利润最大? 最大利润是多少元?
(1)购买一个甲种品牌毽子和一个乙种品牌毽子各需要多少元?
(2)若购买甲、乙两种品牌毽子共花费 1000 元,甲种品牌毽子数量不低于乙种品牌毽子数量的 5 倍且不超过乙种品牌毽子数量的 16 倍,则有几种购买方案?
(3)若商家每售出一个甲种品牌毽子利润是 5 元,每售出一个乙种品牌毽子利润是 4 元,在(2)的条件下,学校如何购买毽子商家获得利润最大? 最大利润是多少元?
答案:
(1)解:设购买一个甲种品牌毽子需要$x$元,一个乙种品牌毽子需要$y$元。
$\begin{cases}10x + 5y = 200 \\15x + 10y = 325\end{cases}$
解得
$\begin{cases}x = 15 \\y = 10\end{cases}$
答:购买一个甲种品牌毽子需要15元,一个乙种品牌毽子需要10元。
(2)解:设购买甲种品牌毽子$m$个,乙种品牌毽子$n$个。
$15m + 10n = 1000$
化简得$3m + 2n = 200$,$m = \frac{200 - 2n}{3}$。
由题意得
$\begin{cases}\frac{200 - 2n}{3} \geq 5n \\frac{200 - 2n}{3} \leq 16n\end{cases}$
解得$\frac{200}{50} \leq n \leq \frac{200}{17}$,即$4 \leq n \leq 11\frac{13}{17}$。
$n$为正整数且$200 - 2n$是3的倍数,$n = 4, 7, 10$。
对应$m = 64, 62, 60$。
答:有3种购买方案。
(3)解:利润$W = 5m + 4n$,将$m = \frac{200 - 2n}{3}$代入得
$W = 5×\frac{200 - 2n}{3} + 4n = \frac{1000 - 10n + 12n}{3} = \frac{1000 + 2n}{3}$。
$W$随$n$增大而增大,当$n = 10$时,$W$最大,$W = \frac{1000 + 20}{3} = 340$。
答:购买甲种品牌毽子60个,乙种品牌毽子10个时商家获得利润最大,最大利润是340元。
(1)解:设购买一个甲种品牌毽子需要$x$元,一个乙种品牌毽子需要$y$元。
$\begin{cases}10x + 5y = 200 \\15x + 10y = 325\end{cases}$
解得
$\begin{cases}x = 15 \\y = 10\end{cases}$
答:购买一个甲种品牌毽子需要15元,一个乙种品牌毽子需要10元。
(2)解:设购买甲种品牌毽子$m$个,乙种品牌毽子$n$个。
$15m + 10n = 1000$
化简得$3m + 2n = 200$,$m = \frac{200 - 2n}{3}$。
由题意得
$\begin{cases}\frac{200 - 2n}{3} \geq 5n \\frac{200 - 2n}{3} \leq 16n\end{cases}$
解得$\frac{200}{50} \leq n \leq \frac{200}{17}$,即$4 \leq n \leq 11\frac{13}{17}$。
$n$为正整数且$200 - 2n$是3的倍数,$n = 4, 7, 10$。
对应$m = 64, 62, 60$。
答:有3种购买方案。
(3)解:利润$W = 5m + 4n$,将$m = \frac{200 - 2n}{3}$代入得
$W = 5×\frac{200 - 2n}{3} + 4n = \frac{1000 - 10n + 12n}{3} = \frac{1000 + 2n}{3}$。
$W$随$n$增大而增大,当$n = 10$时,$W$最大,$W = \frac{1000 + 20}{3} = 340$。
答:购买甲种品牌毽子60个,乙种品牌毽子10个时商家获得利润最大,最大利润是340元。
5. 某单位给某乡中小学提供一批饮用水和蔬菜共 320 件,其中饮用水比蔬菜多 80 件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共 8 辆,一次性将这批饮用水和蔬菜全部运往该乡中小学. 已知每辆甲种货车最多可装饮用水 40 件和蔬菜 10 件,每辆乙种货车最多可装饮用水和蔬菜各 20 件,则运输部门安排甲、乙两种货车时有几种方案? 请你帮助设计出来.
(3)在(2)的条件下,如果甲种货车每辆需付运费 400 元,乙种货车每辆需付运费 360 元. 运输部门应选择哪种方案可使运费最少? 最少运费是多少元?
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共 8 辆,一次性将这批饮用水和蔬菜全部运往该乡中小学. 已知每辆甲种货车最多可装饮用水 40 件和蔬菜 10 件,每辆乙种货车最多可装饮用水和蔬菜各 20 件,则运输部门安排甲、乙两种货车时有几种方案? 请你帮助设计出来.
(3)在(2)的条件下,如果甲种货车每辆需付运费 400 元,乙种货车每辆需付运费 360 元. 运输部门应选择哪种方案可使运费最少? 最少运费是多少元?
答案:
【解析】:
(1)此题可以通过设置一元一次方程来解决。设蔬菜有$x$件,则饮用水有$x + 80$件。根据题目描述,两者总数为320,因此可以列出方程$x + (x + 80) = 320$。
(2)此题需要利用不等式组来求解。设租用甲种货车$m$辆,则乙种货车有$8 - m$辆。根据货车的装载量和货物的数量,可以列出两个不等式:
$40m + 20(8 - m) \geq 240$ (装饮用水的数量)
$10m + 20(8 - m) \geq 80$ (装蔬菜的数量)
解这个不等式组可以得到$m$的取值范围,从而确定租车方案。
(3)此题需要计算各方案的总运费,并找出最少运费的方案。总运费可以表示为$W = 400m + 360(8 - m)$,其中$m$为甲种货车的数量。通过计算不同$m$值下的$W$,可以找出最少运费的方案。
【答案】:
(1)解:设蔬菜有$x$件,则饮用水有$x + 80$件。
由题意,$x + (x + 80) = 320$,
解得$x = 120$,
所以饮用水有$x + 80 = 200$件,蔬菜有120件。
(2)解:设租用甲种货车$m$辆,则乙种货车有$8 - m$辆。
由题意,列出不等式组:
$\begin{cases}40m + 20(8 - m) \geq 200 \\10m + 20(8 - m) \geq 120\end{cases}$
解这个不等式组,得到:
$2 \leq m \leq 4$
由于$m$为正整数,因此$m$可以取2,3,4,即有三种方案:
方案一:甲种货车2辆,乙种货车6辆;
方案二:甲种货车3辆,乙种货车5辆;
方案三:甲种货车4辆,乙种货车4辆。
(3)解:总运费$W = 400m + 360(8 - m) = 40m + 2880$,
由于$40 > 0$,因此$W$随着$m$的增大而增大。
所以当$m = 2$时,$W$取得最小值,即$W = 40 × 2 + 2880 = 2960$元。
因此,运输部门应选择甲车2辆,乙车6辆,这样可以使运费最少,最少运费是2960元。
(1)此题可以通过设置一元一次方程来解决。设蔬菜有$x$件,则饮用水有$x + 80$件。根据题目描述,两者总数为320,因此可以列出方程$x + (x + 80) = 320$。
(2)此题需要利用不等式组来求解。设租用甲种货车$m$辆,则乙种货车有$8 - m$辆。根据货车的装载量和货物的数量,可以列出两个不等式:
$40m + 20(8 - m) \geq 240$ (装饮用水的数量)
$10m + 20(8 - m) \geq 80$ (装蔬菜的数量)
解这个不等式组可以得到$m$的取值范围,从而确定租车方案。
(3)此题需要计算各方案的总运费,并找出最少运费的方案。总运费可以表示为$W = 400m + 360(8 - m)$,其中$m$为甲种货车的数量。通过计算不同$m$值下的$W$,可以找出最少运费的方案。
【答案】:
(1)解:设蔬菜有$x$件,则饮用水有$x + 80$件。
由题意,$x + (x + 80) = 320$,
解得$x = 120$,
所以饮用水有$x + 80 = 200$件,蔬菜有120件。
(2)解:设租用甲种货车$m$辆,则乙种货车有$8 - m$辆。
由题意,列出不等式组:
$\begin{cases}40m + 20(8 - m) \geq 200 \\10m + 20(8 - m) \geq 120\end{cases}$
解这个不等式组,得到:
$2 \leq m \leq 4$
由于$m$为正整数,因此$m$可以取2,3,4,即有三种方案:
方案一:甲种货车2辆,乙种货车6辆;
方案二:甲种货车3辆,乙种货车5辆;
方案三:甲种货车4辆,乙种货车4辆。
(3)解:总运费$W = 400m + 360(8 - m) = 40m + 2880$,
由于$40 > 0$,因此$W$随着$m$的增大而增大。
所以当$m = 2$时,$W$取得最小值,即$W = 40 × 2 + 2880 = 2960$元。
因此,运输部门应选择甲车2辆,乙车6辆,这样可以使运费最少,最少运费是2960元。
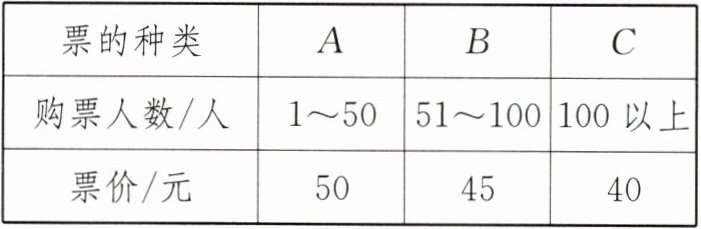
6. 新情境 购买门票 (2023·聊城中考)今年五一小长假期间,我市迎来了一个短期旅游高峰. 某热门景点的门票价格规定见下表:
| 票的种类 | A | B | C |
| :------- | :------ | :------- | :-------- |
| 购票人数/人 | 1~50 | 51~100 | 100 以上 |
| 票价/元 | 50 | 45 | 40 |
某旅行社接待的甲、乙两个旅游团共 102 人(甲团人数多于乙团). 在打算购买门票时,如果把两团联合作为一个团体购票会比两团分别各自购票节省 730 元.
(1)求两个旅游团各有多少人?
(2)一个人数不足 50 人的旅游团,当游客人数最低为多少人时,购买 B 种门票比购买 A 种门票节省?
| 票的种类 | A | B | C |
| :------- | :------ | :------- | :-------- |
| 购票人数/人 | 1~50 | 51~100 | 100 以上 |
| 票价/元 | 50 | 45 | 40 |

某旅行社接待的甲、乙两个旅游团共 102 人(甲团人数多于乙团). 在打算购买门票时,如果把两团联合作为一个团体购票会比两团分别各自购票节省 730 元.
(1)求两个旅游团各有多少人?
(2)一个人数不足 50 人的旅游团,当游客人数最低为多少人时,购买 B 种门票比购买 A 种门票节省?
答案:
【解析】:
(1)本题可先判断出甲、乙两团的人数范围,再设出甲、乙两团的人数,根据“两团联合作为一个团体购票比两团分别各自购票节省$730$元”列出方程,进而求解两团人数。
判断甲、乙两团人数范围:
已知甲、乙两个旅游团共$102$人(甲团人数多于乙团),且两团联合作为一个团体购票比两团分别各自购票节省$730$元。
因为两团总人数$102\gt100$,所以两团联合购票时,每张门票$40$元。
设甲团有$x$人,则乙团有$(102 - x)$人,因为甲团人数多于乙团,所以$x\gt51$,$102 - x\lt50$。
设未知数并列出方程:
设甲团有$x$人,乙团有$(102 - x)$人。
甲团人数$x$满足$51\leqslant x\leqslant100$,此时甲团票价为$45$元/人;乙团人数$102 - x$满足$1\leqslant102 - x\leqslant50$,此时乙团票价为$50$元/人。
两团联合购票费用为$40×102$元,两团分别购票费用为$45x + 50(102 - x)$元。
根据“两团联合作为一个团体购票比两团分别各自购票节省$730$元”,可列方程:
$45x + 50(102 - x) - 40×102 = 730$
解方程:
$45x + 5100 - 50x - 4080 = 730$
$-5x + 1020 = 730$
$-5x = 730 - 1020$
$-5x = -290$
$x = 58$
则乙团人数为$102 - 58 = 44$(人)。
所以,甲团有$58$人,乙团有$44$人。
(2)本题可通过设未知数,根据“购买$B$种门票比购买$A$种门票节省”列出不等式,进而求解该旅游团的最低人数。
设这个旅游团有$m$人($m\lt50$)。
购买$A$种门票的费用为$50m$元,购买$B$种门票的费用为$45m$元。
根据“购买$B$种门票比购买$A$种门票节省”,可列不等式:
$45m\lt50m - 50× 1$(这里$50× 1$表示至少节省$1$元,因为人数是整数,节省的费用也至少是$1$元的整数倍)
$50 - 45m\gt0$
$5m\gt50$
$m\gt 45÷5$
$m\gt 45× \frac{1}{5}$
解得$m\gt 45×\frac{1}{1} = 45$,
因为$m$为正整数,所以$m$的最小值为$46$。
再加上$1$人,即$46 + 1 = 46$(当$m = 45$时,$45×50 = 2250$,$45×45 = 2025$,$2250 - 2025 = 225\gt0$,不满足节省的条件,所以人数要大于$45$),当$m = 46$时,$46×50 = 2300$,$46×45 = 2070$,$2300 - 2070 = 230\gt0$,满足条件。
所以,当这个旅游团人数最低为$46$人时,购买$B$种门票比购买$A$种门票节省。
【答案】:
(1)甲团有$58$人,乙团有$44$人;
(2)$46$。
(1)本题可先判断出甲、乙两团的人数范围,再设出甲、乙两团的人数,根据“两团联合作为一个团体购票比两团分别各自购票节省$730$元”列出方程,进而求解两团人数。
判断甲、乙两团人数范围:
已知甲、乙两个旅游团共$102$人(甲团人数多于乙团),且两团联合作为一个团体购票比两团分别各自购票节省$730$元。
因为两团总人数$102\gt100$,所以两团联合购票时,每张门票$40$元。
设甲团有$x$人,则乙团有$(102 - x)$人,因为甲团人数多于乙团,所以$x\gt51$,$102 - x\lt50$。
设未知数并列出方程:
设甲团有$x$人,乙团有$(102 - x)$人。
甲团人数$x$满足$51\leqslant x\leqslant100$,此时甲团票价为$45$元/人;乙团人数$102 - x$满足$1\leqslant102 - x\leqslant50$,此时乙团票价为$50$元/人。
两团联合购票费用为$40×102$元,两团分别购票费用为$45x + 50(102 - x)$元。
根据“两团联合作为一个团体购票比两团分别各自购票节省$730$元”,可列方程:
$45x + 50(102 - x) - 40×102 = 730$
解方程:
$45x + 5100 - 50x - 4080 = 730$
$-5x + 1020 = 730$
$-5x = 730 - 1020$
$-5x = -290$
$x = 58$
则乙团人数为$102 - 58 = 44$(人)。
所以,甲团有$58$人,乙团有$44$人。
(2)本题可通过设未知数,根据“购买$B$种门票比购买$A$种门票节省”列出不等式,进而求解该旅游团的最低人数。
设这个旅游团有$m$人($m\lt50$)。
购买$A$种门票的费用为$50m$元,购买$B$种门票的费用为$45m$元。
根据“购买$B$种门票比购买$A$种门票节省”,可列不等式:
$45m\lt50m - 50× 1$(这里$50× 1$表示至少节省$1$元,因为人数是整数,节省的费用也至少是$1$元的整数倍)
$50 - 45m\gt0$
$5m\gt50$
$m\gt 45÷5$
$m\gt 45× \frac{1}{5}$
解得$m\gt 45×\frac{1}{1} = 45$,
因为$m$为正整数,所以$m$的最小值为$46$。
再加上$1$人,即$46 + 1 = 46$(当$m = 45$时,$45×50 = 2250$,$45×45 = 2025$,$2250 - 2025 = 225\gt0$,不满足节省的条件,所以人数要大于$45$),当$m = 46$时,$46×50 = 2300$,$46×45 = 2070$,$2300 - 2070 = 230\gt0$,满足条件。
所以,当这个旅游团人数最低为$46$人时,购买$B$种门票比购买$A$种门票节省。
【答案】:
(1)甲团有$58$人,乙团有$44$人;
(2)$46$。
查看更多完整答案,请扫码查看


