《2025年实验班提优训练八年级数学上册浙教版》

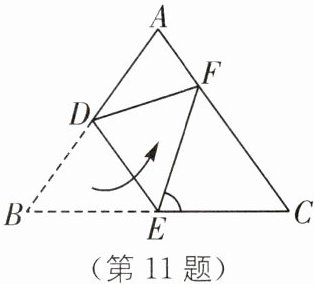
11.(2025·重庆长寿区期末)如图,在$\triangle ABC$中,$AB= AC$,把$\triangle ABC$沿线段 DE 折叠,使点 B 落在点 F 处,若$AC// DE$,$\angle CEF= \alpha$,则$\angle ADF$的度数(结果用含$\alpha$的式子表示)为(D).

A.$60^\circ+2\alpha$
B.$90^\circ-\alpha$
C.$180^\circ-\alpha$
D.$180^\circ-2\alpha$

答案： D　[解析]
∵把△ABC沿线段DE折叠，使点B落在点F 处,∠CEF=α,
∴∠DEB=∠DEF=$\frac{1}{2}$×(180°−α)=90°−$\frac{1}{2}$α,∠BDE=∠FDE.
∵AC//DE,
∴∠DEB=∠C=90°−$\frac{1}{2}$α.
∵AB=AC,
∴∠B=∠C=90°−$\frac{1}{2}$α,
∴∠BDE=180°−(90°−$\frac{1}{2}$α)−(90°−$\frac{1}{2}$α)=α=∠FDE,
∴∠ADF=180°−∠BDE−∠FDE=180°−2α.故选D.

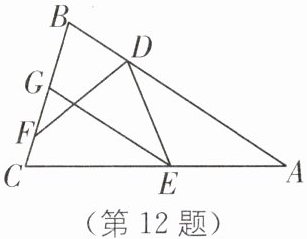
12.(湖北武汉自主招生)如图,在$\triangle ABC$中,$AB= AC$,D,E 分别为 AB,AC 上的点,$\angle BDE$,$\angle CED$的平分线分别交 BC 于点 F,G,$EG// AB$,若$\angle BGE= 100^\circ$,则$\angle ADE$的度数为(B).

A.$18^\circ$
B.$20^\circ$
C.$25^\circ$
D.$30^\circ$

答案： B　[解析]
∵EG//AB,∠BGE=100°,
∴∠B=180°−∠BGE =80°,∠CEG=∠A,∠GED=∠ADE.
∵AB=AC,
∴∠C=∠B=80°,∠A=180°−∠B−∠C=20°,
∴∠CEG=∠A=20°.
∵EG平分∠CED,
∴∠GED=∠CEG=20°,
∴∠ADE=∠GED=20°.故选B.

13. 新情境 数学与生活融合 如图,AOB 是一钢架,设$\angle AOB= \alpha$,为了使钢架更加坚固,需在其内部添加一些钢管 EF,FG,GH,…,添加的钢管长度都与 OE 相等,若最多能添加这样的钢管 5 根,则$\alpha$的取值范围是______.

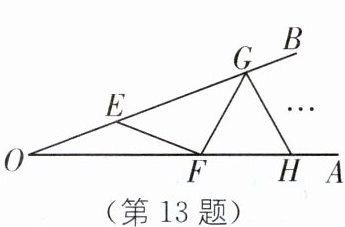
答案：
15°≤α＜18°　[解析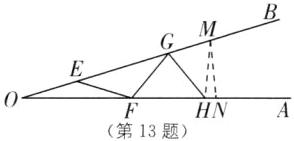]如图.　　
∵OE=EF,
∴∠EOF=∠EFO=α,
∴∠GEF=∠EOF+∠EFO=2α,　　同理可得∠GFH=3α,∠HGM=4α,∠MHA=5α.
∵最多能添加这样的值钢管5根，
∴5α＜90°,6α≥90°,
∴15°≤α＜18°.

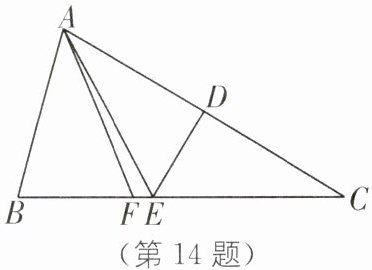
14.(2024·宁波北仑区期中)如图,在$\triangle ABC$中,AF 平分$\angle BAC$,AC 的垂直平分线交 BC 于点 E,$\angle B= 75^\circ$,$\angle FAE= 18^\circ$,则$\angle C= $23度.

答案： 23　[解析]
∵DE是AC的垂直平分线，
∴EA=EC,
∴∠EAC=∠C.
∵∠FAE=18°,
∴∠FAC=∠EAC+18°=∠C+18°.
∵AF平分∠BAC,
∴∠BAF=∠FAC=∠C+18°.
∵∠B+∠BAC+∠C=180°,
∴75°+∠C+18°+∠C+18°+∠C=180°,　　解得∠C=23°.

15.(2024·宁波海曙区期中)如图,已知点 P 为$\angle AOB$的平分线上 的一点,点 D 在边 OA 上.在边 OB 上取一点 E,使得$PE= PD$,设$\angle OEP为\alpha$,$\angle ODP为\beta$,则$\alpha与\beta$的数量关系是______.

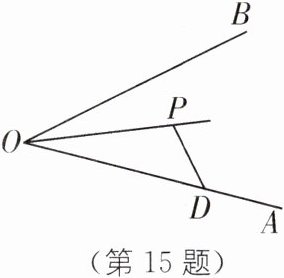
答案：
α=β或α+β=180°　[解析]如图，以点O为圆心，以OD 为半径作弧,交OB于点E₂,连结PE₂.　　OE₂=OD,　　在△E₂OP和△DOP中,∠E₂OP=∠DOP,　　OP=OP,
∴△E₂OP≌△DOP(SAS),
∴E₂P=PD,　　即此时点E₂符合条件,此时∠OE₂P=∠ODP,即α=β.　　 　　以点P为圆心，以PD为半径作弧，交OB于另一点E₁，连结PE₁,　　则PD=PE₁.
∵PE₂=PE₁=PD,
∴∠PE₂E₁=∠PE₁E₂.
∵∠OE₁P+∠PE₁E₂=180°,∠OE₂P=∠ODP,
∴∠OE₁P+∠ODP=180°,即α+β=180°,
∴∠OEP与∠ODP所有可能的数量关系是α=β或α+β=180°.

16.(2024·杭州翠苑中学期中)已知:如图,点 B,D,E,C 在同一直线上,$AB= AC$,$AD= AE$.求证:$BD= CE$.

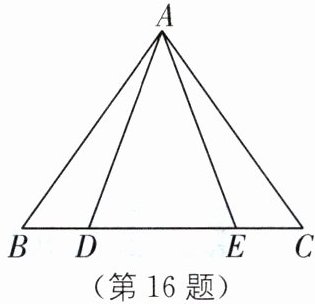
答案：
∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED.　又∠ADE=∠B+∠BAD,∠AED=∠C+∠CAE,
∴∠BAD=∠CAE.　在△ABD和△ACE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS),所以BD=CE.

17. 如图,在$\triangle ABC$中,$\angle A= 40^\circ$,点 D,E 分别在边 AB,AC 上,$BD= BC= CE$,连结 CD,BE.
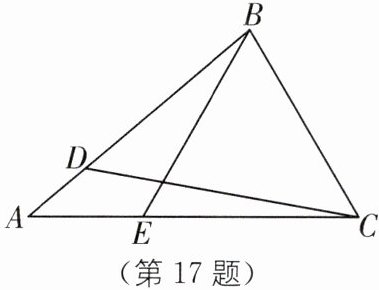
(1)若$\angle ABC= 80^\circ$,求$\angle BDC$,$\angle ABE$的度数;
(2)写出$\angle BEC与\angle BDC$之间的关系,并说明理由.

答案：
(1)
∵∠ABC=80°,BD=BC,
∴∠BDC=∠BCD=$\frac{1}{2}$×(180°−80°)=50°.
∵在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°,
∴∠ACB=180°−80°−40°=60°.
∵CE=BC,
∴∠EBC=$\frac{1}{2}$×(180°−60°)=60°,
∴∠ABE=∠ABC−∠EBC=20°.　
(2)∠BEC+∠BDC=110°.理由如下:　设∠BEC=α,∠BDC=β.　在△ABE中,α=∠A+∠ABE=40°+∠ABE.
∵CE=BC,
∴∠CBE=∠BEC=α,
∴∠ABC=∠ABE+∠CBE=∠ABE+∠BEC=∠A+2∠ABE=40°+2∠ABE.
∵在△BDC中,BD=BC,
∴∠BDC=∠BCD=β,
∴∠BDC+∠BCD+∠DBC=2β+40°+2∠ABE=180°,
∴β=70°−∠ABE,
∴α+β=40°+∠ABE+70°−∠ABE=110°,
∴∠BEC+∠BDC=110°.