《2025年全优方案夯实与提高七年级数学下册北师大版》

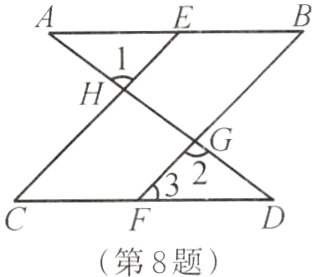
8. 如图，已知AD分别与AB，CD交于点A，D，EC，BF与AB，CD交于点E，C，B，F，且∠1=∠2，∠B=∠C。
(1)求证：CE//BF。
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗？若能，写出你得出结论的过程；若不能，请说明理由。

答案：
(1)
∵∠1 = ∠CHG,∠1 = ∠2,
∴∠CHG = ∠2。
∴CE//BF。
(2) 能。理由如下:
∵CE//BF,
∴∠C = ∠3。
∵∠B = ∠C,
∴∠B = ∠3。
∴AB//CD。
∴∠A = ∠D。

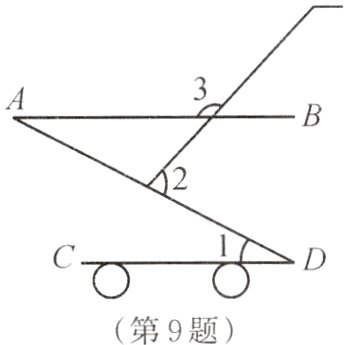
9. 如图是一款手推车的平面示意图，其中AB//CD，∠1=26°，∠2=74°，那么∠3的度数为( )。

A. 100°
B. 132°
C. 142°
D. 154°

答案： B

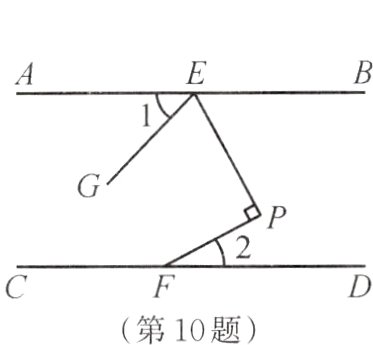
10. 如图，已知AB//CD，点E，F分别在直线AB，CD上，∠EPF=90°，∠BEP=∠GEP，则∠1与∠2的数量关系为( )。

A. ∠1=∠2
B. ∠1=2∠2
C. ∠1=3∠2
D. ∠1=4∠2

答案： B

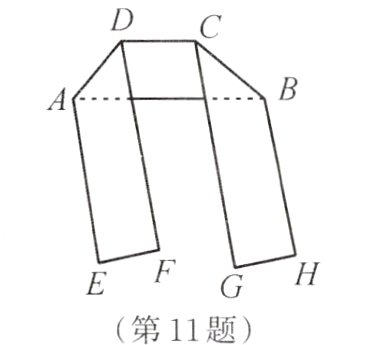
11. 一条两边沿互相平行的围巾按如图的方式折叠，已知∠DAB - ∠ABC=10°，且DF//CG，则3∠DAB+2∠ABC=________。

答案： $230^{\circ}$

12. 如图，已知AB//CD//EF，∠B=60°，∠D=10°，EG平分∠BED，则∠GEF=________。

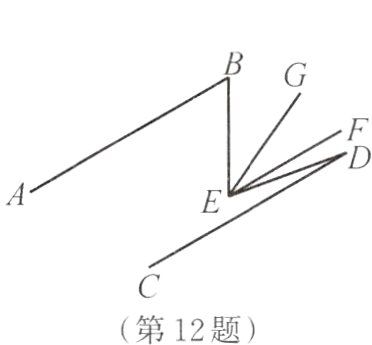
答案： $25^{\circ}$

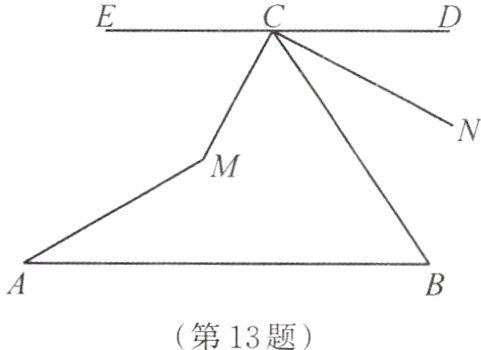
13. 如图，AB//CD，∠NCM=90°，∠NCB=28°，∠MAB=30°，CM平分∠BCE。求：
(1)∠B的度数。
(2)∠AMC的度数。

答案：
(1)
∵∠NCM = 90°,∠NCB = 28°,
∴∠MCB = ∠NCM - ∠NCB = 62°。
∵CM平分∠ECB,
∴∠MCB = ∠ECM = 62°。
∴∠DCB = 180° - ∠MCB - ∠ECM = 56°。
∵AB//DE,
∴∠B = ∠DCB = 56°。
(2) 过点M作MG//AB。
∵AB//CD,
∴AB//CD//MG。
∴∠CMG = 180° - ∠ECM = 118°,∠AMG = ∠MAB = 30°。
∴∠AMC = ∠CMG + ∠AMG = 148°。