《2025年全优方案夯实与提高七年级数学下册北师大版》

9. 已知$1\ nm = 10^{-9}\ m$，某种植物花粉颗粒的直径为35000 nm，则这种花粉颗粒的直径为( )。
A. $3.5\times10^{-5}\ m$
B. $3.5\times10^{4}\ m$
C. $3.5\times10^{-9}\ m$
D. $3.5\times10^{-6}\ m$

答案： A

10. 已知$(\frac{1}{3})^{-m}=2,\frac{1}{3^{n}} = 5$，则$9^{2m - n}$的值为( )。
A. 100
B. $\frac{16}{25}$
C. 200
D. 400

答案： D

11. (1)已知$0.0000283 = 2.83\times10^{x}$，则$x =$________。(2)已知$100 = 0.1^{x}$，则$x =$________。

答案：
(1)-5
(2)-2

12. 若$\vert x - 2\vert=(2x - 6)^{0}$，则$x =$________。

答案： 1

13. 阅读材料：①1的任何次幂都为1；② - 1的奇数次幂为 - 1；③ - 1的偶数次幂为1；④任何不等于零的数的零次幂都为1。请问当$x$为何值时，代数式$(2x + 3)^{x + 2027}$的值为1。

答案： ①当$2x + 3 = 1$时，$x = -1$。
②当$2x + 3 = -1$时，$x = -2$，
但此时$x + 2027 = 2025$是奇数，$\therefore x\neq -2$。
③当$x + 2027 = 0$时，$x = -2027$，
此时$2x + 3 = -4051\neq 0$。
综上所述，当$x = -1$或$x = -2027$时，代数式$(2x + 3)^{x + 2027}$的值为1。

14. 已知$a^{m}=2,a^{n}=4,a^{k}=32(a\neq0)$。求：
(1)$a^{3m + 2n - k}$的值。
(2)$k - 3m - n$的值。

答案：
(1)$\because a^{3m}=2^{3}$，$a^{2n}=4^{2}=2^{4}$，$a^{k}=32 = 2^{5}$，
$\therefore a^{3m + 2n - k}=a^{3m}\cdot a^{2n}\div a^{k}=2^{3}\cdot 2^{4}\div 2^{5}=2^{3 + 4 - 5}=2^{2}=4$。
(2)$\because a^{k - 3m - n}=2^{5}\div 2^{3}\div 2^{2}=2^{0}=1 = a^{0}$，
$\therefore k - 3m - n = 0$。

15.【绥化】定义一种新的运算：若$a\neq0$，则有$a▲b = a^{-2}+ab+\vert -b\vert$，那么$(-\frac{1}{2})▲2$的值是( )。

A. - 3
B. 5
C. $-\frac{3}{4}$
D. $\frac{3}{2}$

答案： B

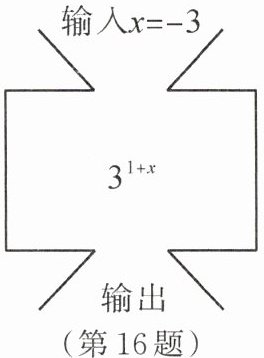
16.【镇江】如图，根据数值转换机的示意图，输出的值为________。

答案： $\frac{1}{9}$

17. 已知$a = 2^{-4444},b = 3^{-3333},c = 5^{-2222}$，请用“＜”把它们按从小到大的顺序连接起来，请说明理由。

答案： $b\lt c\lt a$。理由如下：
$a=(2^{-4})^{11111}=(\frac{1}{2^{4}})^{11111}=(\frac{1}{16})^{11111}$，
$b=(3^{-3})^{11111}=(\frac{1}{3^{3}})^{11111}=(\frac{1}{27})^{11111}$，
$c=(5^{-2})^{11111}=(\frac{1}{5^{2}})^{11111}=(\frac{1}{25})^{11111}$，
$\because\frac{1}{16}＞\frac{1}{25}＞\frac{1}{27}$，
$\therefore(\frac{1}{16})^{11111}＞(\frac{1}{25})^{11111}＞(\frac{1}{27})^{11111}$。$\therefore b\lt c\lt a$。